Problema 408

En el triángulo ABC, B=40º, C=20º, D en BC, BD=AC. Hallar <DAC.

Salazar, J. C. (2004): Comunicación personal.

Según los datos la figura sería como sigue:

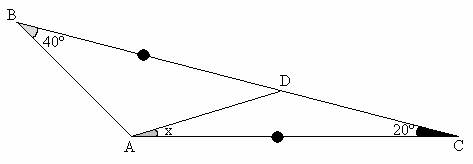
Solución:

*Prolonguemos BA hasta Q de modo tal que AQ = AC.

*De la figura notamos claramente que m<CAQ = 60º.

*Unamos C con Q logrando obtener el triángulo AQC que es equilátero.

*Tracemos la ceviana QP ( P en BC) de modo que m<QPC = 80º, entonces el triángulo QPC es isósceles por tanto QC = QP y la m<PQC = 20º.

*En Q , la m<PQA = 40º.

*Como m<PBQ = m<PQB = 40º por lo tanto el triángulo BPQ es isósceles entonces BP = PQ.

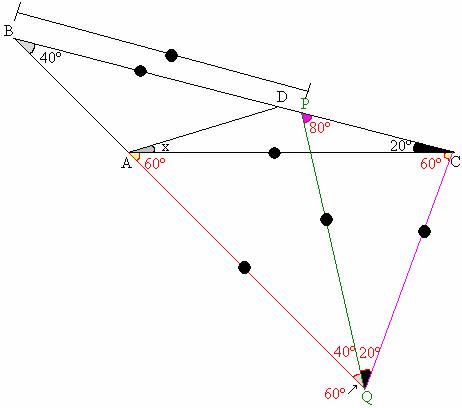
*Sin embargo de la figura misma no es posible que BD = BP ( pues BD < BP) así que la única posibilidad es que los puntos P y D coincidan en un mismo punto ( el punto D), quedando el gráfico Nº1 así:

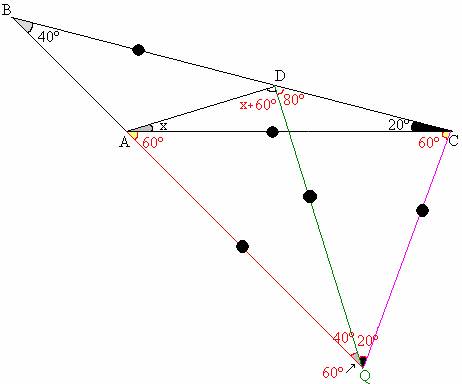
*Notamos que el triángulo AQD es isósceles pues AQ = DQ entonces m<ADQ = x + 60º , por lo tanto en ese mismo triángulo :

x + 60º + x + 60º + 40º = 180º

Finalmente x = 10º

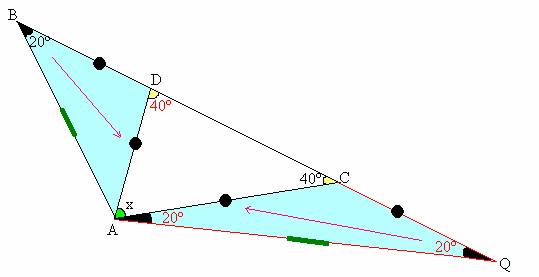
Del problema propuesto hagamos un intercambio respecto a las medidas de los dos ángulos interiores del triángulo ABC que nos dan como dato, obsérvese el cambio:

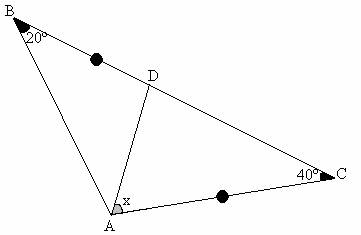
Ha surgido un nuevo problema¡¡¡¡¡¡¡¡¡¡¡¡

Veamos su solución:

*Prolonguemos BC hasta Q de modo que CQ = CA, entonces el triángulo ACQ es isósceles por lo tanto m<CAQ = m<CQA = 20º.

*Entonces el triángulo BAQ es isósceles luego BA = QA.

*Se nota que el triángulo ABD es congruente con el triángulo AQC ( criterio LAL).

Por lo tanto : AD = AC.

*Luego el triángulo ADC es isósceles, siendo m<ACD = m<CDA = 40º.

Entonces: x +40º + 40º = 180º ,finalmente x = 50º.

Huaral, 15 de Enero de 2007

Julio Miranda Ubaldo

Profesor de Matemáticas