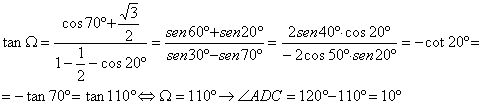Problema 408.- (Propuesto por Juan Carlos Salazar, profesor de geometría del equipo olímpico de Venezuela).

Resolución: (Vicente Vicario García, Huelva)

            Consideremos el triángulo ABC dado y el punto D en el lado BC de forma que . Sin pérdida de generalidad supondremos . Denominaremos , y  .

Aplicando el teorema de los senos al triángulo ABD  se tiene:   .

Aplicando el teorema de los senos al triángulo ADC  se tiene: 

ya que .

            Igualando ahora los dos valores de x anteriores entonces

           

            Desarrollando el seno de la suma de dos ángulos en la última expresión y considerando el seno del ángulo doble  y relaciones trigonométricas elementales, se tiene

                       

                       

                       

            Finalmente, utilizando las fórmulas de transformación de productos de razones trigonométricas (senos y/o cosenos) en sumas y relaciones trigonométricas elementales