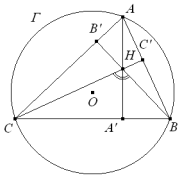
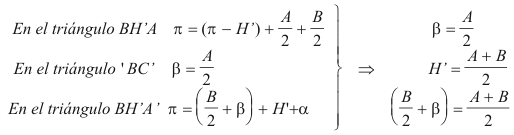De investigación. Problema 409

LUGARES GEOMÉTRICOS DE TRIÁNGULOS INSCRITOS EN UN CÍRCULO

Sea un círculo Γ de centro O. Sobre su circunferencia, se toman dos puntos fijos B y C que son los dos vértices de la base de un triángulo ABC inscrito en el círculo Γ.

1. Si el vértice A recorre la circunferencia de Γ, hallar el lugar geométrico del ortocentro H del triángulo ABC.
   
   
2. Sean A’, B’, C’ las intersecciones de la circunferencia de Γ respectivamente con las bisectrices internas de los ángulos A, B, C. Si el vértice A recorre la circunferencia de Γ, hallar el lugar geométrico del ortocentro H ’ del triángulo A’B’C’.
   
   

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de octubre de 2007)

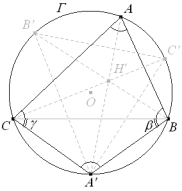
Si el vértice A recorre la circunferencia de Γ, hallar el lugar geométrico del ortocentro H del triángulo ABC.

Dibujamos el ortocentro H, para una posición cualquiera del vértice A.

figura 1

Calculamos ahora la magnitud del ángulo BHC, para ello debemos tener en cuenta que

y sustituyendo estos valores en el triángulo HBC, obtenemos

despejamos el ángulo BHC

pero el ángulo en A es constante al ser constante la cuerda BC, ello significa que el ángulo π - A también es constante y por lo tanto podemos deducir que H recorre el arco capaz de ángulo π - A sobre el segmento BC.

figura 2

• Este arco será el opuesto por BC al arco capaz de ángulo A que trazamos.
  
• Por C, recta que forma con BC un ángulo A. Perpendicular a esa recta por C.
  
• Trazamos la mediatriz del segmento BC que corta a la perpendicular anterior en el centro del círculo que contiene los arcos capaces mencionados.

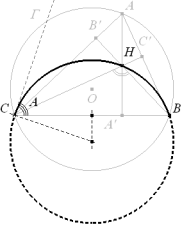
Cuando A recorre la parte opuesta al segmento BC el lugar es el arco que completa el círculo mencionado y que aparece discontinuo en la figura.

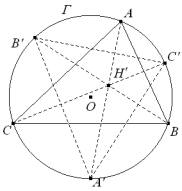
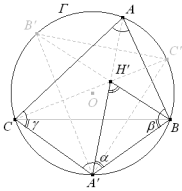
Sean A’, B’, C’ las intersecciones de la circunferencia de Γ respectivamente con las bisectrices internas de los ángulos A, B, C. Si el vértice A recorre la circunferencia de Γ, hallar el lugar geométrico del ortocentro H’ del triángulo A’B’C’.

Dibujemos H’ para una posición cualquiera de A.

figura 3

¿ Cómo es el triángulo A’BC ?

figura 4

Como el cuadrilátero ABA’C está inscrito en el círculo Γ, los ángulos opuesto son suplementarios.

Además AA’ es la bisectriz del ángulo A lo que significa que A’ es el punto medio del arco opuesto por BC; ya que el segmento A’B y el segmento A’C se ven desde A bajo los ángulos respectivos

y como a ángulos iguales corresponden arcos iguales y a arcos iguales corresponden segmentos iguales tenemos que

y por lo tanto el triángulo A’BC es isósceles y así sus ángulos iguales valen

¿ Cómo es el triángulo BH’A’ ?

figura 5

Estudiemos los distintos ángulos

entonces

y por lo tanto el triángulo BH’A’ es isósceles, de lo que se desprende

pero como también hemos visto que el triángulo A’BC, es isósceles, nos queda que

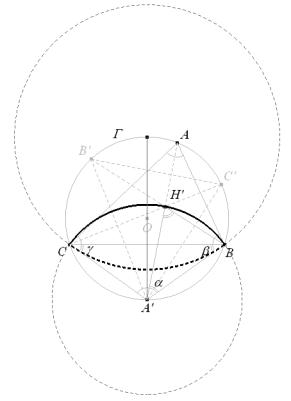
 B, C, H’ equidistan de A’ y por lo tanto pertenecen a un mismo círculo que pasa por B y C con centro en A’ y este será el lugar buscado.

figura 6

Cuando A recorra el arco opuesto al segmento BC, A’ será el punto diametralmente opuesto al actual y el arco a considerar será el que aparece a trazos en la figura.