De investigación

Propuesto por José María Pedret. Ingeniero Naval. (Esplugas de Llobregat, Barcelona)

Problema 409

LUGARES GEOMÉTRICOS DE TRIÁNGULOS INSCRITOS EN UN CÍRCULO

Sea un círculo Γ de centro O. Sobre su circunferencia, se toman dos puntos fijos B y C que son los dos vértices de la base de un triángulo ABC inscrito en el círculo Γ.

1. Si el vértice A recorre la circunferencia de Γ, hallar el lugar geométrico del ortocentro H del triángulo ABC.
2. Sean A’, B’, C’ las intersecciones de la circunferencia de Γ respectivamente con las bisectrices internas de los ángulos A, B, C. Si el vértice A recorre la circunferencia de Γ, hallar el lugar geométrico del ortocentro H’ del triángulo A’B’C’.

José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona)

Solución.-

1.-

Primera demostración

Trazo una línea a través de B, h₁ (es una altura). La perpendicular a ella por C alcanza a la circunferencia circunscrita en el vértice A₁. Por C trazo la perpendicular a BA₁ (otra altura h’₁). El punto de corte es el ortocentro de A₁BC y un punto del lugar geométrico buscado. De este modo se establece una correspondencia entre el haz de rectas por B, B* y el haz de rectas por C, C*. Por su definición se trata de una proyectividad. El lugar geométrico que buscamos es, pues, una cónica, y pasa por los vértices fijos B y C.

En esta proyectividad puede suceder que la perpendicular por C no corte a la circunscrita, por ser tangente a ella, en este caso el vértice A se confunde con C. Tal sucede cuando la altura por B es paralela al radio OC, la recta h₂ en el dibujo. Le corresponde en C*

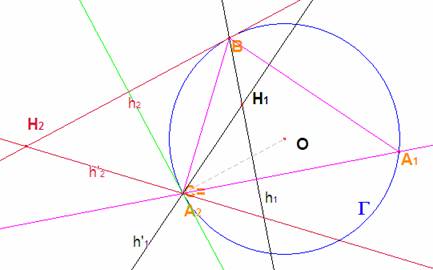
la recta h’₂ perpendicular a BA₂= BC por C.

Si trazamos la mediatriz de BC, cada triángulo ABC y su simétrico respecto de esa mediatriz poseen ortocentros que también son simétricos: esta mediatriz es un eje de simetría de la cónica investigada.

Pongamos ahora que el punto A sea uno de los puntos comunes a la circunferencia y a esta mediatriz. El triángulo ahora es isósceles y la altura desde A es también mediana. Sabemos que el simétrico del ortocentro respecto al punto medio de cada lado se encuentra sobre la circunferencia circunscrita.

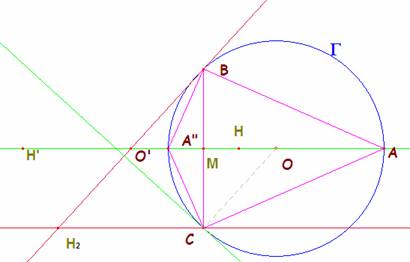
Por tanto, H y H’ (simétricos respecto a BC de A” y A respectivamente) son los ortocentros de los triángulos ABC y A”BC. Si HH’ es un eje de la cónica, el punto medio O’ es su centro, equidistante de B y C por estar en su mediatriz.

Ya tenemos muchos datos de la cónica: Puntos H, H’, B, C y H₂, centro O’. También conocemos un eje (y el otro, perpendicular por O’). Falta saber qué tipo de cónica es. Se podía haber construido el ortocentro para el caso en que A coincide B y tendríamos un punto más. Pero no es necesario.

Los puntos H’ y H por simetría respecto a BC se transforman en A y A”: son congruentes los triángulos H’HB y AA”B. Resulta que BO’= CO’=BO=O’H =O’H’. Se trata de una circunferencia de igual radio que G. Sus centros son simétricos respecto del lado fijo BC (pues M es también punto medio de AH’)

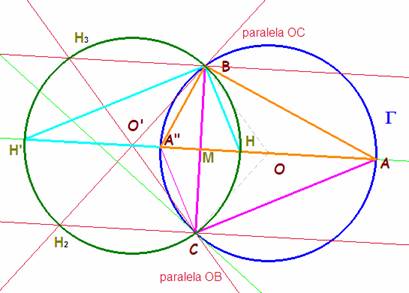
Segunda demostración

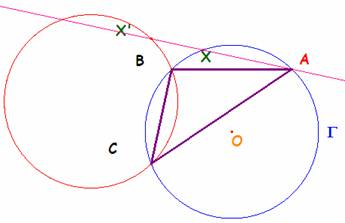
El simétrico del ortocentro respecto de cada lado yace en la circunferencia circunscrita. Tomo X sobre G. Llamo X' a su simétrico respecto BC. Éste es el ortocentro de un triángulo ABC. El vértice A es el otro punto donde la perpendicular por X' a BC encuentra a G.

Recíprocamente, por cada punto A de G, la perpendicular a BC corta otra vez a G. Su simétrico respecto BC es el ortocentro del triángulo.

Por tanto la asignación X --> A es biunívoca.

De todo ello se deduce que el lugar geométrico de los ortocentros es la circunferencia simétrica respecto BC de G, su radio es el de ésta y su centro el simétrico de O.

2.

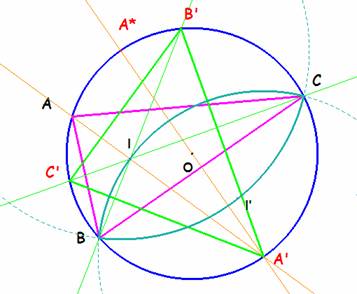
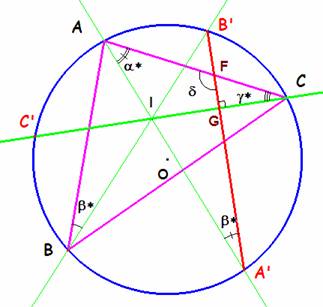
Queremos probar que la bisectriz de C es perpendicular a A’B’ y en consecuencia, el ortocentro de A’B’C’ es el incentro I de ABC. Denotamos por a*, b* y g* los ángulos mitad de A, B y C respectivamente. Observando el triángulo AA’F (donde F es la intersección de A’B’ con AC) el ángulo en A’ mide b* por abarcar el arco AB’ y el ángulo en F, d mide 90 + g* por ello el ángulo FGC es recto como se pretendía demostrar.

El lugar geométrico del ortocentro de A’B’C’ es el lugar del incentro de ABC. En el problema 285 de esta revista establecimos que “el lugar geométrico del incentro de un triángulo con dos vértices fijos B y C y el otro A variable sobre un arco de circunferencia que pasa por B y C es otro arco de circunferencia que pasa por los puntos fijos y que tiene su centro en el punto medio P del arco BC que no tiene al otro vértice”.

Los arcos BA’C y CB’B completan la circunferencia circunscrita. Los centros de los arcos que describe el incentro se encuentran en los extremos del diámetro mediatriz de BC. Uno de esos extremos es A’ pues la bisectriz se encuentra con la mediatriz del lado opuesto en la circunferencia circunscrita. El otro A*, está sobre la bisectriz exterior de A. Así pues tendremos los puntos A’ y A* como centros de los dos arcos que forman el lugar geométrico del incentro de ABC o bien del ortocentro de A’B’C’.