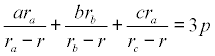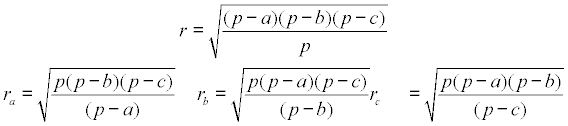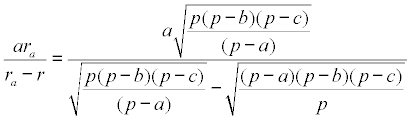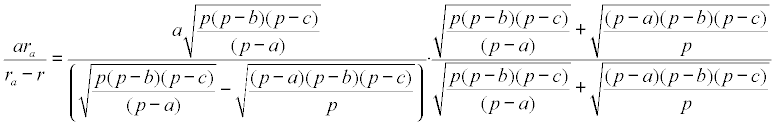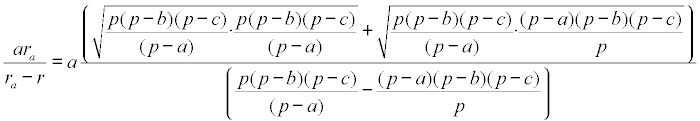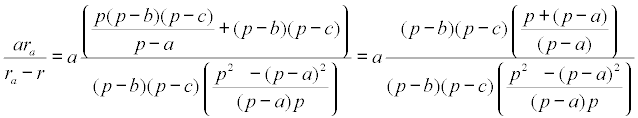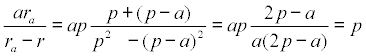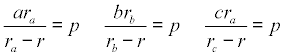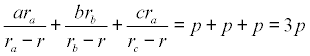De investigación. Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 410. Demostrar la fórmula

Donde r_a, r_b, r_c, son los radios de los círculos ex-inscritos, al triángulo ABC, respectivamente, y p el semi-perímetro.

Lemoine, E. (1900) El progreso matemático (2) II, p. 336 (Cuestión 343). Zaragoza
Lemoine, E. (1902) Revista Trimestral de Matemáticas, Año II, Diciembre N. 8 p. 192. Zaragoza.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (18 de octubre de 2007)

SOLUCIÓN

Para llegar a la demostración propuesta daremos por sabidas las siguientes expresiones

En función de lo anterior, expresamos el primer sumando como

que sin cambiar la ecuación podemos escribir como

y operando en el numerador y el denominador respectivamente, obtenemos

donde ejecutando las raíces cuadradas nos queda

y eliminando los factores comunes del numerador y el denominador llegamos a

y por simetría con los otros sumandos del primer miembro de la ecuación propuesta

que nos conduce a

como queríamos demostrar.