Problema 410

Demostreu que  on , ,  són els radis dels cercles exinscrits, r el radi del cercle inscrit i p el semiperímetre del triangle .

Lemoine, E. (1900) El progreso matemático (2) II, p. 336 (Cuestión 343). Zaargoza

Lemoine, E. (1902) Revista Trimestral de Matemáticas, Año II, Diciembre N. 8 p. 192. Zaragoza.

Solució:

La proporció entre els radis de les circumferències inscrita i exinscrites al triangle  és:

,  ,  .

.

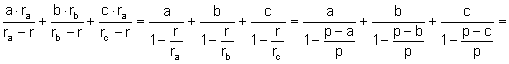
Propietat: Proporció entre els radis de les circumferències inscrites i exinscrites.

Siga el triangle .

Siguen r i  els radis de les circumferències inscrita i exinscrita, respectivament.

Aleshores,     on p és el semiperímetre del triangle

Demostració:

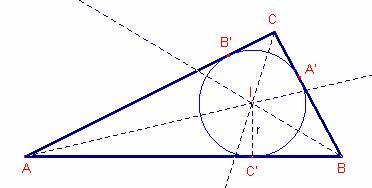
Siguen els punts A’, B’, C’ els punts de tangència de la circumferència inscrita al triangle  amb els costats.

Aleshores,

Per tant

Anàlogament,

Siga la circumferència exinscrita de centre  i radi .

Siguen A”, B”, C” els punts de tangència de la circumferència inscrita al triangle  amb les prolongacions dels costats.

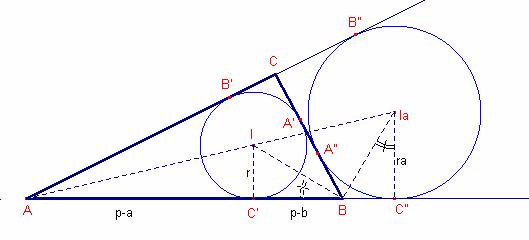
Calculem  i

Aleshores;   

                  

Sumant les expressions:

, aleshores,  

Per tant,  

Els triangle ,  són semblants, aleshores,

Anàlogament, ,  .