Problema 410

Demostrar que  donde , ,  son los radios de los círculos exinscritos, r el radio del círculo inscrito y p el semiperímetro del triángulo .

Lemoine, E. (1900) El progreso matemático (2) II, p. 336 (Cuestión 343). Zaargoza

Lemoine, E. (1902) Revista Trimestral de Matemáticas, Año II, Diciembre N. 8 p. 192. Zaragoza.

Solución de Ricard Peiró:

La proporción entre los radios de las circunferencias inscrita y exinscritas del triángulo  es:

,  ,  .

.

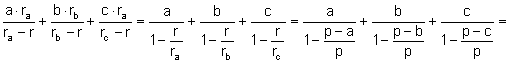
Propiedad: Proporción entre los radios de las circunferencias inscritas y exinscritas.

Sea el triángulo .

Sean r y  los radios de las circunferencias inscrita y exinscrita, respectivamente.

Entonces,     donde p es el semiperímetro del triángulo

Demostración:

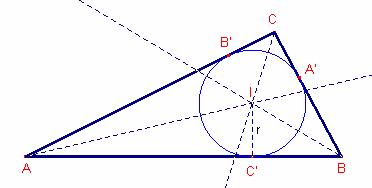
Sean A’, B’, C’ los puntos de tangencia de la circunferencia inscrita al triángulo  con los lados.

Entonces,

Por tanto

Análogamente,

Sea la circunferencia exinscrita de centro  y radio .

Sean A”, B”, C” los puntos de tangencia de la circunferencia inscrita al triángulo  con las prolongaciones de los lados.

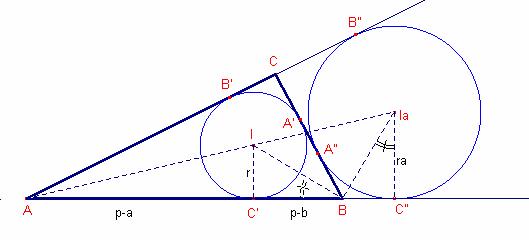
Calculemos  y

Entonces;   

                  

Sumando las expresiones:

, entonces,  

Por tanto,  

Los triángulos ,  son semejantes, entonces,

Análogamente, ,  .