De investigación
Propuesto por José María Pedret. Ingeniero Naval. (Esplugas de Llobregat, Barcelona)
Problema 411
LUGARES GEOMÉTRICOS DE TRIÁNGULOS INSCRITOS EN UN CÍRCULO
Sea un círculo Γ de centro O. Sobre su circunferencia, se toman dos puntos fijos B y C que son los dos vértices de la base de un triángulo ABC inscrito en el círculo Γ.
1.- Si el vértice A recorre la circunferencia de Γ,
hallar el lugar geométrico del baricentro G del triángulo ABC
Resuelto por JULIÁN SANTAMARÍA TOBAR profesor de Dibujo
del IES
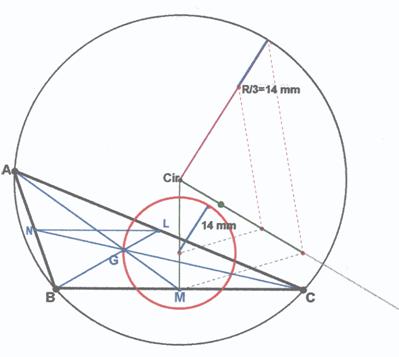
El baricentro G está a 1/3 de la mediana. Deducción: N y L son los puntos medios de los lados AB y AC, por lo tanto los triángulos ANL y el ABC son homotéticos de razón ½. Þ NL=BC/2. Los triángulos BCG y LNG también son homotéticos con razón -1/2 porque NL=BC/2 Þ NG = GC/2 =Mediana/3.
Considerando fijo el punto medio M de BC, el punto A se puede trasformar en el baricentro G mediante una homotecia de razón 1/3 siendo el centro de homotecia el punto M. Si el vértice A recorre la circunferencia la figura homotética de la circunferencia será otra circunferencia. Luego el lugar geométrico de los posibles baricentros corresponde a una circunferencia de radio igual a 1/3 del radio de la circunferencia circunscrita cuyo centro está a 1/3 del segmento M-Cir (punto medio M del lado BC y el circuncentro Cir)
2.- Se traza la altura hB desde el vértice B,
que corta al lado CA en el punto D, y la altura hC
desde el vértice C que corta al lado AB en el punto E.
Unimos D con E y determinamos un punto P tal que
PE/PD=k
Si el vértice A recorre la circunferencia de Γ, hallar el lugar
geométrico de P.
Resuelto por JULIÁN SANTAMARÍA TOBAR profesor de Dibujo
del IES
Antes de ver la posición de un punto cualquiera P, supongamos
que el punto P es el punto medio M entre DE, o sea M es tal que ME/MD=1/2
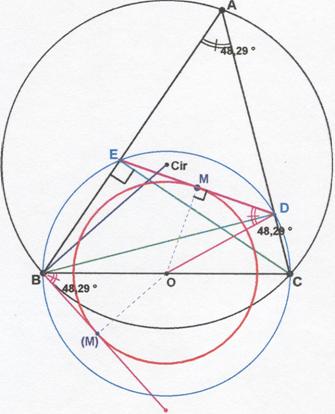
El punto D es pie de la altura hB trazada desde el vértice B al lado CA y está en un arco capaz de 90º del lado BC. El punto E correspondiente a la altura hC también está en el mismo arco capaz. El segmento ED es una cuerda de la circunferencia de diámetro BC, esta cuerda ED tiene una longitud constante aunque el vértice A se desplace por la circunferencia circunscrita. La medida de un ángulo exterior a la circunferencia es igual a la semidiferencia de los arcos comprendidos entre sus lados. En el dibujo el ángulo A, aunque se desplace por la circunferencia, es constante porque abarca la misma cuerda; uno de los arcos comprendidos por los lados del ángulo A en la circunferencia de diámetro BC es la semicircunferencia (también constante) por lo tanto el arco abarcado por ED tiene que ser constante para que la igualdad de la semidiferencia se mantenga. Por lo tanto queda demostrado que la cuerda ED no varía de longitud. En consecuencia cualquier punto P que pertenezca al segmento ED formará una circunferencia concéntrica a la de diámetro BC.
El ángulo MDO mide lo mismo que el ángulo A. El cuadrilátero BCDE es inscriptible por lo tanto el ángulo EDC = 180-B por ser suplementarios los ángulos B y D. El triángulo OCD es isósceles luego el valor de ODC es C. Por lo tanto MDO = EDC – ODC = 180-B-C = A.
Para trazar la circunferencia correspondiente al lugar geométrico del punto medio M del segmento ED, se puede dibujar el triángulo rectángulo OMD girado hasta hacerle coincidir con el O(M)B. El ángulo OB(M) mide A, luego es el ángulo semi-inscrito a la circunferencia circunscrita y el lado tangente será perpendicular al radio Cir-B de la circunferencia circunscrita.
En definitiva, dada la circunferencia circunscrita de centro Cir,
dos vértices B y C del triángulo y un punto P tal que PE/PD=k, Se
halla el punto medio O entre B y C, por B se hace una perpendicular al segmento
Cir-B y por O una paralela al mismo segmento, estas rectas se cortan en el
punto (M). B-(M) es una posición del semi-segmento ED, se
sitúa P en la relación k y la circunferencia pedida será la que tenga centro en
O y pase por P.