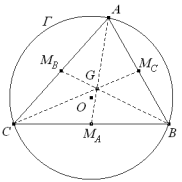
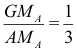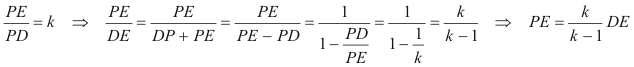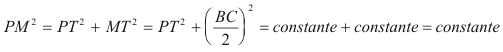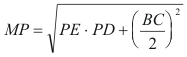LUGARES GEOMÉTRICOS DE TRIÁNGULOS INSCRITOS EN UN CÍRCULO

Sea un círculo Γ de centro O. Sobre su circunferencia, se toman dos puntos fijos B y C que son los dos vértices de la base de un triángulo ABC inscrito en el círculo Γ.

1. Si el vértice A recorre la circunferencia de Γ, hallar el lugar geométrico del baricentro G del triángulo ABC.
   
   
2. Se traza la altura h_B desde el vértice B, que corta al lado CA en el punto D, y la altura h_C desde el vértice C que corta al lado AB en el punto E. Unimos D con E y determinamos un punto P tal que
   
   
   .
   
   Si el vértice A recorre la circunferencia de Γ, hallar el lugar geométrico de P.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (16 de octubre de 2007)

Si el vértice A recorre la circunferencia de Γ, hallar el lugar geométrico del baricentro G del triángulo ABC.

Construimos el enunciado para una posición cualquiera de A,

figura 1

¡¡¡Pero no estudiamos ahora el punto G, estudiamos primero el punto M_B pie de la mediana por B en CA.!!!
M_B es, por definición, el punto medio de CA.

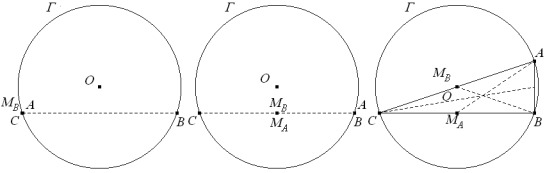
A describe el círculo Γ, en este desplazamiento la recta CA posee un punto fijo que es C; por tanto, M_B describe una figura homotética de la figura que describe A. La razón es ½ y el centro de homotecia es C.

La figura descrita por A es el círculo Γ; por tanto la figura descrita por M_B es otro círculo que determinaremos por tres puntos (ver figura 2); aunque por la homotecia ya sabemos que es el círculo de diámetro OC.

figura 2

• Cuando A coincide con C, también lo hace M_B.
  
• Cuando A coincide con B, M_B coincide com M_A.
  
• Cuando A coincide con el punto de Γ diametralmente opuesto a C, M_B coincide con O.
  

figura 3

Por lo tanto el lugar de M_B es el círculo que pasa por C, M_B y O.

Estudiemos ahora el comportamiento de G al desplazarse M_B

Hemos visto que M_B recorre el círculo de diámetro OC, en ese movimiento la recta M_BB tiene un punto fijo que es B; G el baricentro del triángulo está sobre la recta M_BB además sabemos que

entonces podemos concluir que G es la imagen de M_B por una homotecia de centro B y razón ⅔.

figura 4

Por lo tanto el lugar geométrico de G es un círculo cuyo centro encontramos por la homotecia mencionada y que pasa por el punto G. Si r es el radio del círculo circunscrito a ABC el radio ρ del círculo lugar es el que nos queda después de las dos homotecias puestas de manifiesto

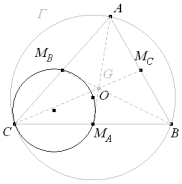
Nota: (Otra construcción)
Si consideramos la mediana AM_A, el punto M_A permanece fijo al recorrer A el círculo Γ. Además sabemos que

Entonces el lugar de G es el círculo homotético de Γ con centro de homotecia en M_A y razón 1/3.

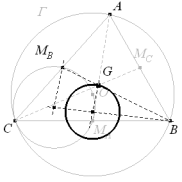
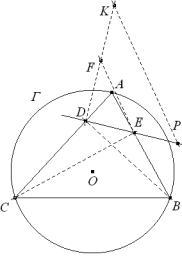
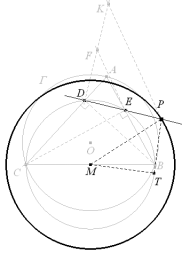
Se traza la altura h_B desde el vértice B, que corta al lado CA en el punto D, y la altura h_C desde el vértice C que corta al lado AB en el punto E. Unimos D con E y determinamos un punto P tal que

.

Si el vértice A recorre la circunferencia de Γ , hallar el lugar geométrico de P.

Dibujamos el enunciado para una posición cualquiera de A.

figura 5

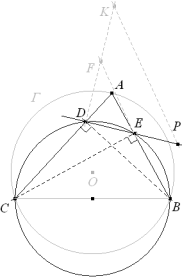
Definimos k, tomando sobre una recta perpendicular por D a DE un punto fijo F y otro punto V tal que

 

figura 6

Las alturas trazadas forman ángulos rectos con los lados respectivos, lo que significa que D y E están sobre el círculo de diámetro BG. Entonces, expresado el ángulo A respecto a este último círculo

Pero como A recorre el círculo Γ y BC es fijo, A es de valor constante y eso nos lleva a deducir que el arco(DE) es constante, lo que a su vez comporta que DE es constante.

Ahora bien

que nos indica que PE es constante y en consecuencia, PD también lo es.

figura 7

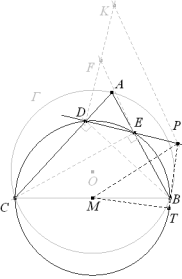
De la constancia de PE y PD, se deprende que la potencia de P respecto al círculo de diámetro BC es constante

Pero

de lo que se deduce que PM también es constante y por lo tanto

figura 8

 el lugar geométrico de P es un círculo de centro M punto medio de BC y radio