Problema 411
LUGARES GEOMÉTRICOS DE TRIÁNGULOS INSCRITOS EN UN CÍRCULO
Sea un círculo Γ de centro O. Sobre su circunferencia, se toman dos puntos fijos B y C que son los dos vértices de la base de un triángulo ABC inscrito en el círculo Γ.
1.- Si el vértice A recorre la circunferencia de Γ, hallar el lugar geométrico del baricentro G del triángulo ABC.
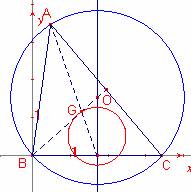
Solución de Ricard Peiró (parte primera):
Consideremos los puntos fijos B, C en las siguientes coordenadas:
, 
.
El centro de la circunferencia que pasa por el B y C está en la mediatriz
del segmento 
, 
.
Sea 
el centro de la circunferencia
El radio de la circunferencia es 
.
La ecuación de la circunferencia 
tiene ecuación:
.
Las coordenadas del punto A son:
.
Sea 
el otro valor se resolvería
análogamente.
El baricentro del triángulo 
tiene coordenadas:
.
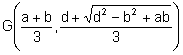Sea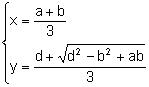 
. 
.
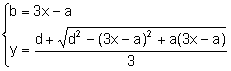. Elevando al cuadrado:
.
.
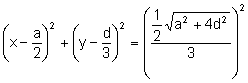Es la circunferencia de centro 
i radio 
, es decir, la circunferencia de radio la tercera parte del radio
de la circunferencia circunscrita al triángulo y de centro en el interior
del triángulo sobre la mediatriz del segmento de tal forma que
divide el segmento formado por el centro de la circunferencia circunscrita al
triángulo y el punto medio de en razón 2:1.