Problema 411.- (Propuesto por J. M. Pedret. Ingeniero Naval).

Sea un círculo de centro O. Sobre su circunferencia se toman dos puntos fijos B y C que son los dos vértices de la base de un triángulo ABC inscrito en el círculo .

1.- Si el vértice recorre la circunferencia, hallar el lugar geométrico del baricentro G del triángulo ABC.

2.- Se traza la altura desde el vértice B que corta al lado CA en el punto D y la altura desde el vértice C que corta al lado AB en el punto E. Unimos D con E y obtenemos un punto P tal que . Si el vértice A recorre la circunferencia , hallar el lugar geométrico que describe el punto P.

Pedret, J. M. (2007): Comunicación personal

Resolución: (Vicente Vicario García, Huelva)

1.- Sea G el baricentro del triángulo ABC. Si M es el punto medio del segmento BC, por la conocida relación que liga a las medianas, se verifica que . Cuando A recorre la circunferencia salvo B y C, entonces G recorre una circunferencia homotética a la dada en una homotecia de centro M y razón , exceptuando los homotéticos de los puntos B y C.

2.- Supondremos aquí que el triángulo ABC es acutángulo, pues los razonamientos que rencia se muestran sólo tienen sentido en esta situación. Aplicaremos varios resultados clásicos conocidos relacionados con el triángulo órtico de otro dado ABC. Sea O el circuncentro del triángulo ABC y R el radio de su circunferencia circunscrita. Sea F el tercer vértice del triángulo órtico de ABC. Sea A´ el punto medio del segmento BC y A´´ el punto medio del segmento DE, lado del triángulo órtico. Es sabido que la mediatriz del segmento DE corta a la bisectriz interior del ángulo F del triángulo órtico en un punto Q que pertenece a la circunferencia que circunscribe al triángulo órtico, es decir, a la circunferencia de los nueve puntos del triángulo ABC. Es sabido también que este punto Q es el punto medio del segmento HA que une el ortocentro H y el vértice A del triángulo.

Además A´ también pertenece a la circunferencia de los nueve puntos y el segmento QA´ es un diámetro de la misma. Según el teorema de Brianchon-Poncelet-Feuerbach, el centro de esta circunferencia es el punto medio de OH del triángulo ABC y su radio es la mitad del radio de la circunferencia circunscrita (entre más resultados), es decir, . Por otra parte, es fácil determinar, aplicando el teorema de los cosenos al triángulo ADE la longitud del segmento , que es constante mientras el vértice A varía sobre la circunferencia original.

Por otra parte tenemos que

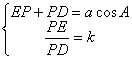
Entonces podemos determinar también

Por otra parte, utilizando propiedades elementales relativas al ángulo inscrito en una circunferencia, la longitud del segmento se calcula fácilmente

Finalmente, podemos determinar la longitud del segmento , y tenemos

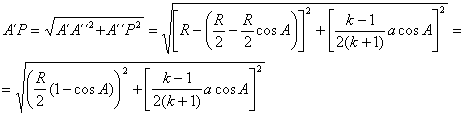
que es constante a medida que el vértice A recorre la circunferencia . Así pues, el lugar geométrico pedido es una circunferencia de centro el punto A´ punto medio del segmento BC y radio A´P determinado anteriormente.