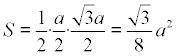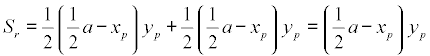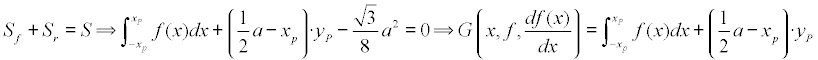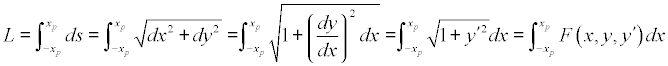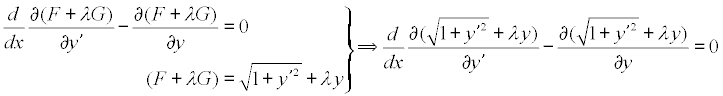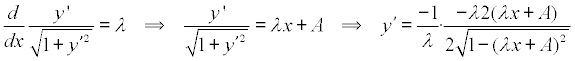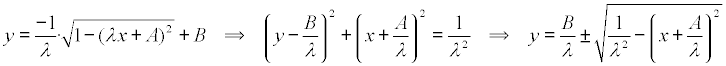|
De investigación. Propuesto por Vicente Vicario García, profesor del I.E.S. El SUR, Huelva Problema 412 Demostrar o refutar si en un triángulo equilátero la curva de longitud mínima que corta al mismo en dos polígonos de igual área, es un segmento de línea recta Vicario, V. (2007): Comunicación personal Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (25 de octubre de 2007) |
|
SOLUCIÓN |
|
|
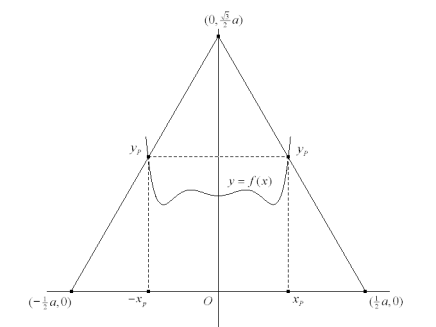
DIBUJAMOS EL ENUNCIADO
Tomamos como eje de ordenadas la altura y como eje de abscisa la base. La simetría del triángulo obliga a la simetría de la curva buscada y=f(x). El área S de medio triángulo equilátero de lado a es
El área bajo la curva y=f(x) es
y el resto del área es
La condición de que la curva divide al triángulo en dos áreas iguales se escribe como
Podemos plantearnos un problema de cálculo de variaciones en el que los límites de integración son variables y existe una ligadura; pero lo que haremos, gracias a la simetría del problema, es la sucesión de dos problemas
CURVA DE MÍNIMA LONGITUD
Con la condición que el área de debajo la curva es una constante
y nos queda
la ecuación de Euler de este problema variacional es
nos queda
resolviendo y’
esta curva es en general una circunferencia, pero por la simetría del problema el centro debe estar en el eje de ordenadas
Por tanto LA CURVA QUE PROPORCIONA LA MÍNIMA LONGITUD ES UNA CIRCUNFERENCIA QUE DEPENDE DE DOS PARÁMETROS (Y NO UNA RECTA); LA DETERMINACIÓN DE LA MISMA SE OBTIENE OBLIGANDO A QUE CUMPLA LA CONDICIÓN SOBRE EL ÁREA QUE NOS DA EL ENUNCIADO |