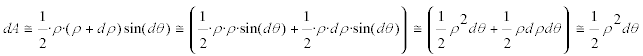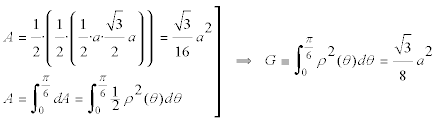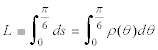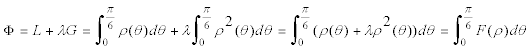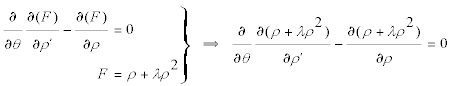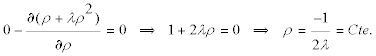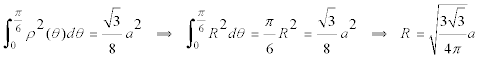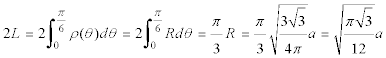|
De investigación. Propuesto por Vicente Vicario García, profesor del I.E.S. El SUR, Huelva Problema 412 Demostrar o refutar si en un triángulo equilátero la curva de longitud mínima que corta al mismo en dos polígonos de igual área, es un segmento de línea recta Vicario, V. (2007): Comunicación personal Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (13 de noviembre de 2007) |
|
SOLUCIÓN |
|
|
DIBUJAMOS EL ENUNCIADO
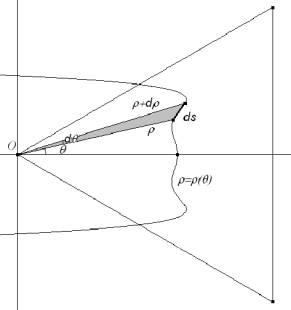
Suponemos que la curva que determina el área está expresada mediante una ecuación explícita en coordenadas polares, con el polo O en el vértice del triángulo equilátero y la altura desde ese vértice como eje θ = 0. EL ÁREA Sabemos que el área del triángulo diferencial de vértice O y base ds tiene por área
y por lo tanto, teniendo en cuenta que el triángulo es equilátero de lado a y que sólo necesitamos media figura (por lo tanto un cuarto de su área, gracias a la simetría), si imponemos la condición del enunciado tendremos
LA LONGITUD Sabemos también que la longitud del arco diferencial de curva es
y por lo tanto la longitud de curva es
PROBLEMA DE MINIMIZACIÓN DE LA LONGITUD CON UNA CONDICIÓN
la ecuación de Euler de este problema variacional es
y nos queda
que nos indica que LAS CURVAS QUE MINIMIZAN EL PROBLEMA SON CIRCUNFERENCIAS DE CENTRO O (Y NO RECTAS). Si además queremos determinar el radio de dichas circunferencias
y la longitud mínima es
|