Problema 412

Demostreu orefuteu si en un triangle equilàter la corba de longitud mínima que talla el triangle en dos polígons d’igual àrea, és un segment de línia recta.

Vicario, V. (2007): Comunicación personal

Solució de Ricard Peiró:

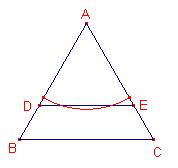Considerem el triangle equilàter de costat 1.

Determinem el mínim segment que talla el triangle equilàter en dos polígons d’igual àrea:

L’àrea del triangle equilàter és .

Siga D un punt del costat i E un punt del costat tal que l’àrea del triangle és la meitat del triangle.

Siga , .

L’àrea del triangle és:

, . Igualant les àrees:

. Simplificant:

.

Aplicant el teorema del cosinus al triangle :

.

.

Considerem la funció .

El mínim de la funció s’assoleix quan .

La distància mínima és, .

Calculem el radi del sector circular amb centre A que divideix el triangle en dues parts d’igual àrea.

, . Igualant les àrees:

.

Resolent l’equació en r:

Calculen la longitud de l’arc de circumferència que forma el sector:

.

. Aleshores el segment no és la mínima corba que divideix el triangle en dues parts d’igual àrea.