Problema 412
Demostrar o refutar si en un triángulo equilátero la curva de longitud mínima que corta al mismo en dos polígonos de igual área, es un segmento de línea recta
Vicario, V. (2007): Comunicación personal
Solución de Ricard Peiró:
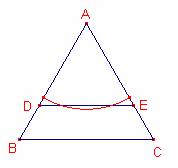 Consideremos
el triángulo equilátero
Consideremos
el triángulo equilátero ![]() de lado 1.
de lado 1.
Determinemos el mínimo segmento que corta el triángulo equilátero en dos polígonos de igual área:
El área del triángulo equilátero es ![]() .
.
Sea D un punto del lado ![]() y E un punto del lado
y E un punto del lado ![]() tal que el área del
triángulo
tal que el área del
triángulo ![]() es la mitad del triángulo.
es la mitad del triángulo.
Sea ![]() ,
, ![]() .
.
El área del triángulo ![]() es:
es:
![]() ,
, ![]() . Igualando las áreas:
. Igualando las áreas:
![]() . Simplificando:
. Simplificando:
![]() .
.
Aplicando el teorema del coseno al triángulo ![]() :
:
![]() .
.
![]() .
.
Consideremos la función ![]() .
.
El mínimo de la función se alcanza cuando ![]() .
.
La distancia mínima es, ![]() .
.
Calculemos el radio del sector circular de centro A que divide el triángulo en dos partes de igual área.
![]() ,
, ![]() . Igualando las áreas:
. Igualando las áreas:
![]() .
.
Resolviendo la ecuación en r:
![]()
Calculemos la longitud del arco de circunferencia que forma el sector:
![]() .
.
![]() . Entonces el segmento no es la mínima curva que divide el
triángulo en dos partes de igual área.
. Entonces el segmento no es la mínima curva que divide el
triángulo en dos partes de igual área.