Resolución: (Vicente Vicario García, Huelva)

            Demostraremos que en contra de la intuición la curva de longitud mínima pedida es la de un arco de circunferencia.

            Inicialmente demostraremos que el segmento de línea recta de longitud mínima que divide en dos polígonos de la misma área a un triángulo equilátero (sin pérdida de generalidad, de lado unidad) es la de una paralela a uno de sus lados de longitud. Para ello emplearemos el análisis matemático y supondremos, también sin pérdida de generalidad que la recta considerada corta a los lados AB y AC en los puntos M  y N, respectivamente.† Sean , . Como el triángulo equilátero debe quedar dividido en dos regiones de la misma área, resulta que

                                              

            Por otra parte, aplicando el teorema de los cosenos al triángulo AMN tenemos  y expresando MN  en función solamente de una variable .

                                              

            Un cálculo rutinario demuestra que la función anterior  presenta un mínimo relativo que a su vez es mínimo absoluto para , ya que

                       

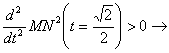                         mínimo relativo

puesto que los valores de la función , que es contínua y derivable en el intervalo en sus extremos son , . Por tanto, el segmento de línea recta buscado es el que proponíamos.

            Demostremos ahora que la curva bisectora de longitud mínima no es la recta sino un arco de circunferencia. Para ello consideremos un hexágono regular de lado unidad. Por el principio isoperimétrico sabemos que de todas las curvas planas cerradas simples (sin autointersecciones) del mismo perímetro, la que abarca área máxima es la circunferencia. Consideremos todas las curvas planas simples cerradas e interiores al hexágono que lo dividen en dos regiones de igual área. Por el principio isoperimétrico, la curva de menor longitud que logra este propósito es la circunferencia y, por tanto, como consecuencia, tenemos que el arco de circunferencia es la curva de longitud mínima que divide en dos partes de igual área a cada uno de los seis triángulos equiláteros que constituyen el hexágono. El radio de la circunferencia bisectora será

                                  

y finalmente, la longitud del arco de circunferencia bisecadora buscada será

                                  

---oooOooo---

Nota: Los valores aproximados hasta la millonésima de los segmento bisecadores lineal y curvilíneo circular determinados son

                                   ;