Problema 413:
En el triángulo ABC, B=80º, C=20º, D en BC, AB=DC.
Hallar <DAC.
Salazar, J. C. (2004): Comunicación
personal
Solución de Alejandro Cipriano Coronel, estudiante de ingeniería de
La grafica del la
figura sería aproximadamente como sigue:
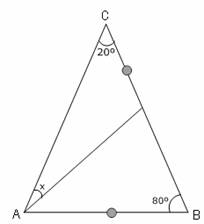
Es claro que el ángulo A es 80º; entonces el triángulo ABC
es isósceles (AC=BC).
Se traza DE, E en AC, tal que DE=DC (m<E=m<C=20º), entonces el ángulo
EDA=20º-x.
Luego se construye el triángulo ADP congruente al triángulo
AED (ED=AP; m<DAP=m<ADE=20º-x)
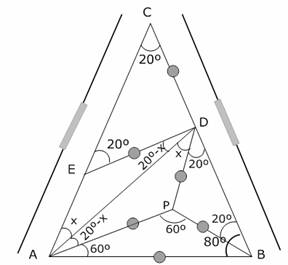
Se sabe que el ángulo A es 80º; además m<EAP=20º;
entonces la m<PAB=60º
Pero AP=AB; entonces al unir P con B se llega a construir
el triángulo APB, dicho triángulo es Equilátero. O sea AB=AP=PB. Por lo tanto
el ángulo PBD=20º.
También es claro que m<PDB=20º, con esto se demuestra
que el triángulo PDB es isósceles
(PD=BP).
Finalmente se ha demostrado que el triángulo APD es
isósceles (AP=PD); Entonces
20º-x = x ; 2x =
20º y de aquí se tiene que: X=10º…. Rpta.