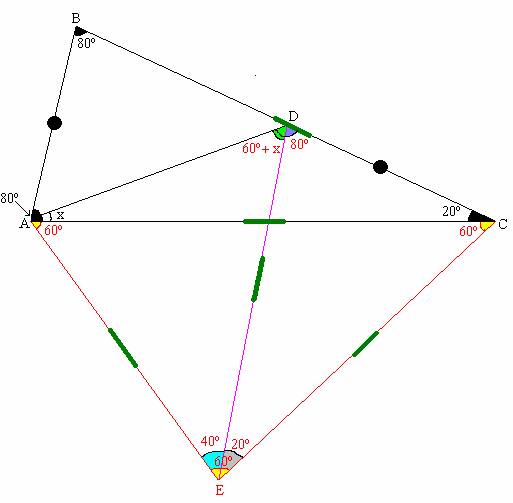
Problema 413 :En el triángulo ABC, B=80º, C=20º, D en BC, AB=DC. Hallar <DAC.
Tres soluciones de Julio A. Miranda Ubaldo, profesor de
Matemáticas de
Según el enunciado del problema , el gráfico es el siguiente:
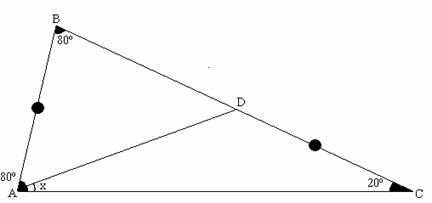
Primer Método de Solución:
*Por simple inspección podemos darnos cuenta que el triángulo ABC es isósceles pues
m<ABC = m<BAC = 80º, por lo tanto BC = AC.
*Se construye el triángulo equilátero BCE , según se muestra en la figura, luego m<ECA = 40º
*Unimos A con E por lo tanto Δ ABE es congruente con el Δ ADC (Criterio LAL)
luego: m<AEB = x.
*De la figura el ΔAEC es isósceles pues AC = EC, por lo tanto
m<AEC = m<EAC = 60º + x , en este mismo triángulo : 60º + x + 60º + x + 40º = 180º
Finalmente x = 10º.
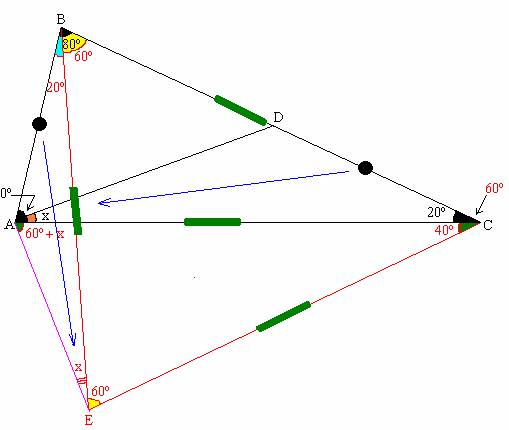
Segundo Método de Solución:
*Sabemos por las razones antes expuestas que el triángulo ABC es isósceles.
*Luego se construye el triángulo ABE, siendo E un punto interior del triángulo ABC,
de acuerdo a la figura. Por tanto m< EBC = 20º.
*Unamos C con E, entonces Δ BEC es congruente con el Δ AEC (Criterio LLL)
luego: m< ECB = m< ECA = 10º.
*De la figura notamos que el Δ EBC es congruente con el Δ ACD (Criterio LAL)
Por lo tanto x = 10º.
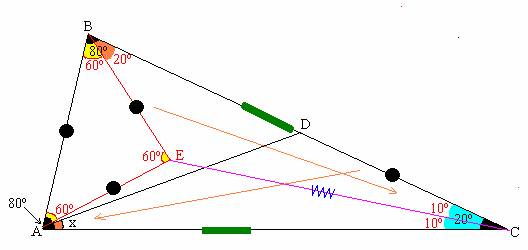
Tercer Método de Solución
*Ya sabemos que el triángulo ABC es isósceles.
*Se construye exteriormente al triángulo ABC el triángulo equilátero AEC.
*Unamos D con E , por lo tanto Δ ABC es congruente con el Δ DCE (Criterio LAL),
entonces AC = DE.
*El triángulo DCE es isósceles pues DE = EC , por consiguiente : m< CDE = 80º y
m< CED = 20º.
*En “E” se observa que m< AED = 40º.
*El triángulo AED es isósceles pues ED =EA , por lo tanto: m< EAD = m< ADE = 60º + x .
*Para finalizar en el triángulo AED : 60º + x + 60º + x + 40º = 180º
Finalmente x = 10º.