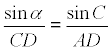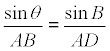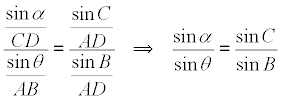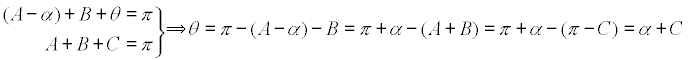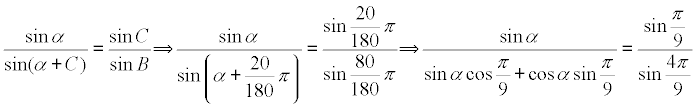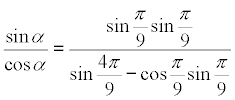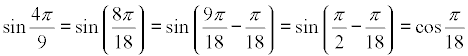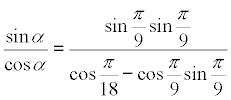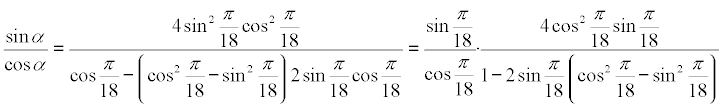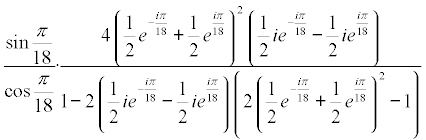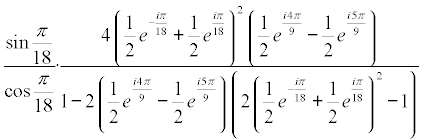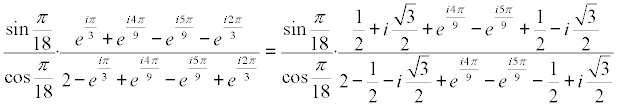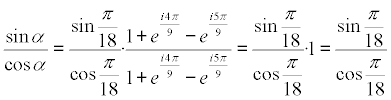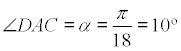|
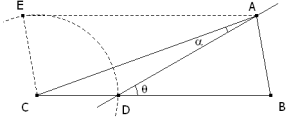
Propuesto por Juan Carlos Salazar, profesor de Geometría del Equipo Olímpico de Venezuela (Puerto Ordaz). Problema 413 En el triángulo ABC, B=80º, C=20º, D en BC, AB=DC. Hallar ∠DAC. Juan Carlos Salazar (2004): Comunicación personal. Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (18 de octubre de 2007) |
|
SOLUCIÓN |
|
ENUNCIADO Por A una paralela a BC y por C una paralela a AB que se cortan en E. Por E arco de radio EC=AB que corta a BC en D.
TEOREMA DE LOS SENOS EN EL TRIÁNGULO CAD
TEOREMA DE LOS SENOS EN EL TRIÁNGULO DAB
LA ECUACIÓN DE PARTIDA Dividiendo miembro a miembro la dos ecuaciones anteriores obtenemos
RELACIÓN ENTRE α y θ
INTRODUCIMOS LOS VALORES DE B Y C
ordenando nos queda
pero
nos lleva a
y utilizando el ángulo mitad
y sustituyendo senos y cosenos por su expresión exponencial compleja
eliminando i de dentro de los paréntesis
y desarrollando los productos
y nos queda
por lo tanto
|