Problema 413.- (Propuesto por Juan Carlos Salazar, profesor de geometría del equipo olímpico de Venezuela).

En el triángulo ABC, , , D en BC, AB=DC. Hallar .

Juan Carlos Salazar (2004): Comunicación personal.

Resolución: (Vicente Vicario García, Huelva)

Denotemos , sin pérdida de generalidad, , , . Obviamente tenemos y .

Aplicando el teorema de los senos al triángulo ABD, tenemos

Aplicando el teorema de los senos al triángulo ADC, tenemos

Despejando x de las dos expresiones anteriores e igualando llegamos a

Desarrollando mediante la expresión del seno de la suma de dos ángulos, entonces

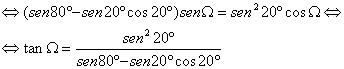
Utilizando ahora las expresiones para el seno, coseno y tangente del ángulo doble, simplificando y empleando relaciones trigonométricas elementales, tenemos que

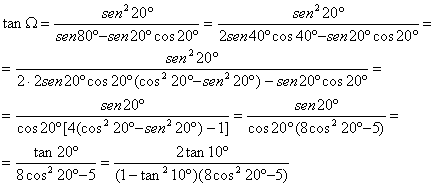
Ahora demostraremos que , ya que . Para ello utilizaremos la identidad trigonométrica del coseno del ángulo doble en función de la tangente del ángulo simple

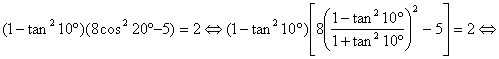
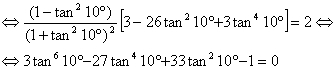
Pero esta última identidad se obtiene fácilmente sustituyendo en la expresión de la tangente del ángulo triple, haciendo . Para ello empleamos las expresiones clásicas para la tangente de la suma de dos ángulos y la tangente del ángulo doble.

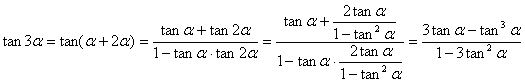
Ahora haciendo tenemos

Finalmente, al elevar al cuadrado obtenemos que

lo que concluye el problema.