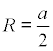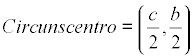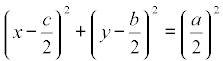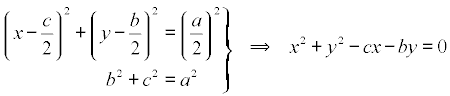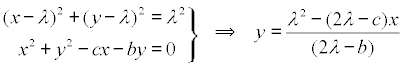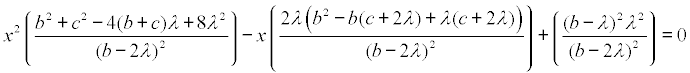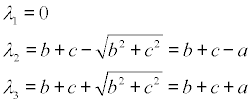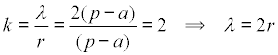|
Para el aula. Propuesto por Ricard Peiró i Estruch Profesor de Matemáticas del IES "Abastos" (València) Problema 414 en español. Demostrar que para cualquier triángulo rectángulo el radio de la circunferencia que entra en contacto con sus catetos y la circunferencia circunscrita (por dentro) es igual al diámetro de la circunferencia inscrita. Problema 414 en català. Demostreu que en qualsevol triangle rectangle el radi de la circumferència que és tangent als catets y tangent interior a la circumferènccia circumcrita és igual al diàmetre de la circumferència inscrita al triangle. Shariguin. “Problemas de Geometría”. Planimetría”. Ed. Mir. Moscú. 1986. problema II106. página 88. Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (22 de octubre de 2007) |
|
| SOLUCIÓN |
|
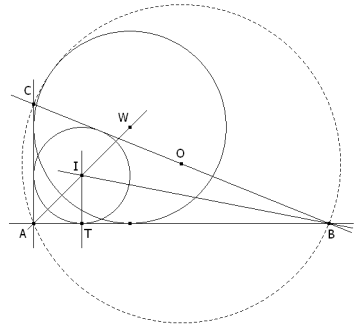 figura 1 ELECCIÓN DE UNOS EJES DE COORDENADAS La ventaja de trabajar con un triángulo rectángulo de lados a=BC, b=CA, c=AB y de semi-perímetro p es que las ecuaciones de los círculos inscrito y circunscrito son bastante simples. Y más sencillas todavía, si tomamos como ejes coordenados los dos catetos, AB como eje de abscisas y AC como eje de ordenadas (origen en A, vértice del ángulo recto). EL CÍRCULO INSCRITO El radio de este círculo es igual a la distancia entre el vértice del ángulo recto y uno de los puntos de contacto que es igual al semi-perímetro menos el lado a.
la ecuación de este círculo es
EL CÍRCULO CIRCUNSCRITO El diámetro de este círculo es el lado BC por lo tanto la mitad de ese lado es el radio
y el centro se halla en el punto medio de ese lado con coordenadas
Como pasa por el origen, la ecuación es
y como el triángulo es rectángulo
EL CÍRCULO TANGENTE A LOS CATETOS E INTERIORMENTE AL CÍRCULO CIRCUNSCRITO La tangencia a los dos catetos, obliga al centro a estar en la bisectriz de tales catetos; el centro ha de ser de la forma
donde λ es el radio desconocido del círculo buscado; lo que indica que la ecuación de este círculo es
El círculo inscrito también es tangente a los catetos y tiene el centro sobre la bisectriz de los mismos. Concluímos que el círculo circunscrito y el círculo buscado son homotéticos en una homotecia de centro A y razón que debemos determinar BUSCAMOS LAS INTERSECCIONES DE ESTE CÍRCULO Y EL CIRCUNSCRITO
que sustituida en la ecuación del círculo circunscrito da
y eliminado el denominador común
polinomio en x, cuyas raíces son las abscisas de las intersecciones entre los dos círculos; si imponemos que la raíz sea doble los puntos de intersección coincidirán en el punto de contacto y en este caso, se anulará el discriminante de la ecuación
que ordenando en potencias de λ queda como
cuyas raíces son
λ1 nos lleva al círculo de centro el origen y de radio nulo, que no es solución y λ3 > λ2 nos indica que λ2 es la solución buscada, pues λ3, al ser mayor es el radio del círculo con tangencia exterior.
CONCLUSIÓN Calculamos ahora la razón buscada
Con este resultado queda también demostrado lo que pide el enunciado. Es decir el radio de la circunferencia que entra en contacto con sus catetos y la circunferencia circunscrita (por dentro) es igual al diámetro de la circunferencia inscrita. |