Problema 414

Demostreu que en qualsevol triangle rectangle el radi de la circumferència que és tangent als catets y tangent interior a la circumferència circumscrita és igual al diàmetre de la circumferència inscrita al triangle.

Solució Ricard Peiró:

Figura barroso414.fig

Applet created on 16/10/07 by User with CabriJava

Considerem el triangle rectangle , .

En circumcentre O del triangle és igual a la meitat de la hipotenusa:

El radi de la circumferència circumscrita és .

El radi r de la circumferència inscrita d’un triangle rectangle és igual al semiperímetre menys la hipotenusa.

.

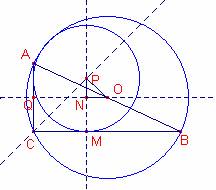
Siga la circumferència tangent als catets i a la circumferència inscrita. El seu centre P es troba en la bisectriu de l’angle C del triangle. Siga x el seu radi.

Per ser les dues circumferències tangents:

.

Considerem la recta perpendicular al catet  que passa per P.

Considerem la recta perpendicular al catet  que passa per O.

Siga N el punt intersecció de les dues rectes.

Siga M la projecció de P sobre el catet .

Siga Q la projecció de O sobre el catet .

Considerem el triangle rectangle , .

.

.

Aplicant el teorema de Pitàgores al triangle :

.

.

Resolent l’equació en la incògnita x:

, aleshores, x és igual al diàmetre de la circumferència inscrita al triangle