Problema 414

Demostrar que para cualquier triángulo rectángulo el radio de la circunferencia que entra en contacto con sus catetos y la circunferencia circunscrita (por dentro) es igual al diámetro de la circunferencia inscrita.

Shariguin. “Problemas de Geometría”. Planimetría”. Ed. Mir. Moscú. 1986. problema II106. página 88.

Solución de Ricard Peiró:

Figura barroso414.fig

Applet created on 16/10/07 by User with CabriJava

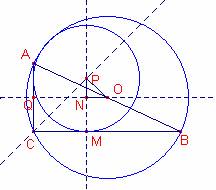Consideremos el triángulo rectángulo , .

En circuncentro O del triángulo es igual a la mitad de la hipotenusa:

El radio de la circunferencia circunscrita es .

El radio r de la circunferencia inscrita de un triángulo rectángulo es igual al semiperímetro menos la hipotenusa.

.

Sea la circunferencia tangente a los catetos y a la circunferencia inscrita. Su centro P se encuentra en la bisectriz del ángulo C del triángulo. Sea x el radio.

Por ser las dos circunferencias tangentes:

.

Consideremos la recta perpendicular al cateto  que pasa por P.

Consideremos la recta perpendicular al cateto  que pasa por O.

Sea N el punto intersección de las dos rectas.

Sea M la proyección de P sobre el cateto .

Sea Q la proyección de O sobre el cateto .

Consideremos el triángulo rectángulo ,

.

.

Aplicando el teorema de Pitágoras al triángulo :

.

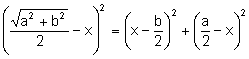Resolviendo la ecuación en la incógnita x:

, entonces, x es igual al diámetro de la circunferencia inscrita al triángulo