Problema 414.- (Propuesto por Ricard Peiró i Estruch, I.E.S. “Abastos”, Valencia).

Demostrar que para cualquier triángulo rectángulo, el radio de la circunferencia que entra en contacto con sus catetos y la circunferencia circunscrita (por dentro) es igual al diámetro de la circunferencia inscrita.

Shariguin. “Problemas de Geometría”. Planimetría”. Ed. Mir. Moscú. 1986. problema II106. página 88.

Resolución: (Vicente Vicario García, Huelva)

Utilizaremos la notación habitual en la geometría del triángulo. Supondremos un triángulo rectángulo de catetos b, c e hipotenusa a (por tanto ) y R, r serán los radios de las circunferencias circunscrita e inscrita al triángulo respectivamente. Sea también el área del triángulo. Inicialmente determinaremos el radio r de la circunferencia inscrita al mismo. Para ello, podemos utilizar cualesquiera de los dos métodos (a) y (b) presentados a continuación

(a) Como [1]

(b) Haciendo siendo r la distancia (radio inscrito) del vértice del ángulo recto a los puntos de contacto de la circunferencia inscrita con los catetos del triángulo ABC y utilizando la equidistancia de las dos tangentes exteriores a una circunferencia desde un punto exterior

[2]

Expresión, obviamente, equivalente a la anterior.

Sean ahora O el radio de la circunferencia circunscrita al triángulo, situado en el punto medio de la hipotenusa y R, su radio, que cumplirá . Sean también O´ y R´ el centro de la circunferencia tangente a los catetos y a la circunferencia circunscrita y su radio, respectivamente. Sea Q el punto de contacto de las circunferencias de centros O y O´. Obviamente los puntos O , O´ y Q están alineados. Sean T y S los puntos de contacto de la circunferencia problema con los catetos c y b respectivamente. Podemos también suponer, sin pérdida de generalidad que . Entonces O´ pertenece a la bisectriz interior del ángulo recto A (formando 45º con los catetos) y , .

Aplicando el teorema de los cosenos al triángulo AOO´, teniendo en cuenta que , y , tenemos que

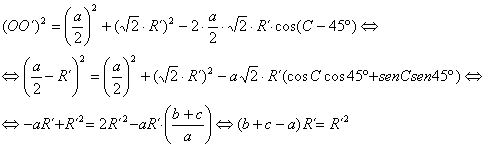
de donde deducimos entonces (comparando con [2]) que , que es lo que se pretendía. La otra solución para R´ corresponde a una solución degenerada.