Problema 415 de triánguloscabri

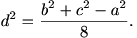
Dado el triángulo ABC, con lados BC=a, CA=b, AB=c, construir la longitud d tal que
Propuesto por Francisco Javier García Capitán y Juan Bosco Romero Márquez.

 

Solución de Francisco Javier García Capitán

Escribimos la relación en la forma

a2 + 8 d2 = b2 + c2

o bien,

2a2 + 16 d2 = 2 b2 + 2 c2.

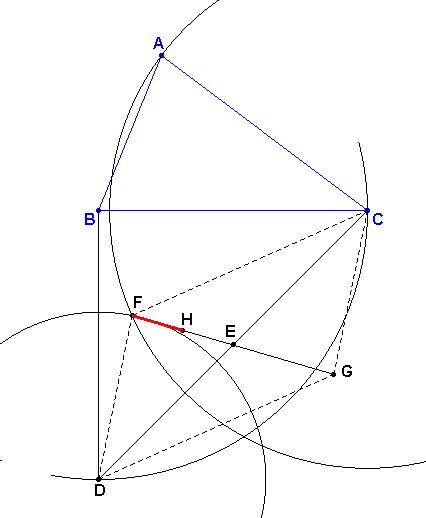
Teniendo en cuenta la identidad del paralelogramo, resulta que 4d es la longitud de una diagonal de un paralelogramo con lados b y c, y la otra diagonal midiendo , lo mismo que la diagonal del cuadado construido con lado a.

Por tanto, la construcción sería como sigue:

  1. Con centro B y radio BC=a trazamos un arco que corta a la perpendicular a BC trazada por B en D. La longitud CD medirá y será una diagonal del paralelogramo.
  2. Trazamos dos circunferencias, una con centro C y radio CA = b , y otra con centro D y radio BA = c. Estas circunferencias se cortan en un punto F. El cuarto vértice G del paralelogramo será el simétrico de F respecto del punto medio E del segmento CD.
  3. La diagonal FG mide 4d, por lo que para hallar d bastará hallar el punto medio H de FE y tendremos FH = HE = d.

 
El problema no tiene solución cuando el triángulo dado es obutsángulo en A, y la construcción falla en ese caso al no existir intersección entre las circunferencias trazadas en el apartado 2.
 

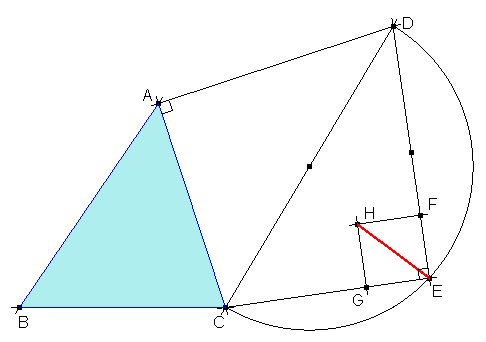
Otra construcción:

Podemos usar de forma progresiva el teorema de Pitágoras.

Primero trazamos AD perpendicular a CA y tal que AD=AB=c.

Tendremos que

Ahora una semicircunferencia con diámetro CD y sobre ella marcamos el punto E tal que CB = CE = a.

Tendremos que

Si marcamos sobre DE el punto F tal que EF es la cuarta parte de ED, entonces la diagonal del cuadrado con longitud EF será