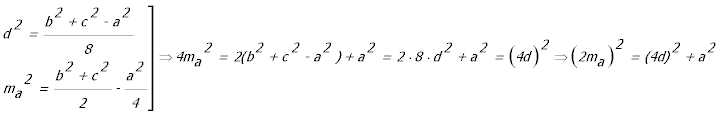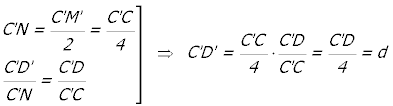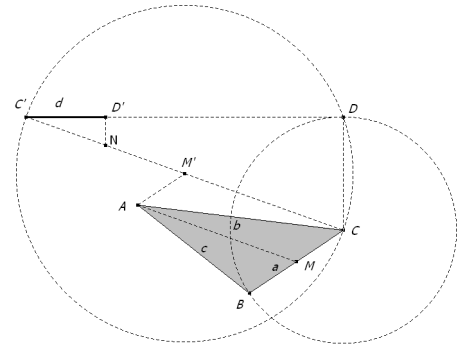
De investigación. Propuesto por Francisco Javier García Capitán , profesor del IES Álvarez Cubero (Priego de Córdoba), y Juan Bosco Romero, profesor colaborador de la Universidad de Valladolid.

Problema 415.

Dado el triángulo ABC, con lados BC=a, CA=b, AB=c, construir la longitud d tal que d²=(b²+c²-a²)/8

García, F.J. y Romero, J.B. (2007): Comunicación personal

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de noviembre de 2007)

SOLUCIÓN

figura 1

Sólo hay que darnos cuenta que la expresión pedida se parece bastante al cuadrado de la mediana por A.

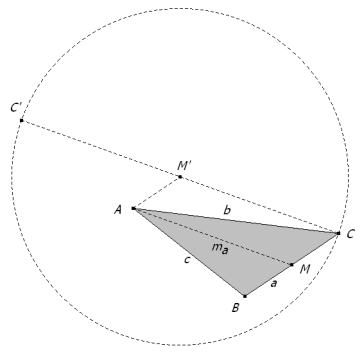
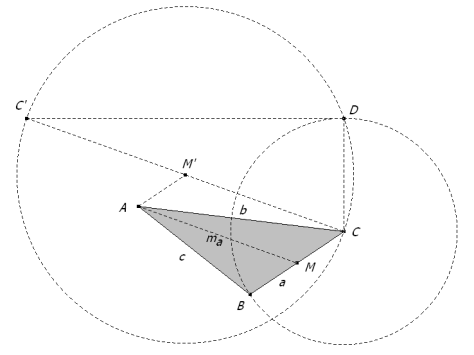
Por lo tanto

d es la cuarta parte del cateto de un triángulo rectángulo cuya hipotenusa es dos veces la mediana por A del triángulo ABC y el otro cateto es a.

Construyamos ese triángulo rectángulo

figura 2

• Por A una recta paralela a BC y por C una recta paralela a AM (la mediana por A ). Estas rectas se cortan en M’.

  
  

  

  
  

• Con centro en M’, circunferencia que pasa por C y corta a M’C en C’

  
  

  

figura 3

• Con centro en C, circunferencia que pasa por B y que corta a la circunferencia anterior en D

  
  

  

figura 4

• Que D esté sobre la circunferencia, nos asegura que el ángulo ∠CDC’ es recto y por lo tanto DC’ es el cateto buscado. De este cateto buscamos la cuarta parte.

  
  

• Sobre CC’ trazamos N, punto medio de M’C’; por N trazamos una recta paralela a CD que corta a DC’ en D’