De investigación

Propuesto por Francisco Javier García Capitán , profesor del IES Álvarez Cubero (Priego de Córdoba), y Juan Bosco Romero, profesor colaborador de la Universidad de Valladolid.

Problema 415.- Dado el triángulo ABC, con lados BC=a, CA=b, AB=c, construir la longitud d tal que d²=(b²+c²- a²)/8.

García, F.J. y Romero, J.B. (2007): Comunicación personal.

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca

Según el teorema del coseno se tiene b²+c²- a² = 2bc·cos A, y de ahí 4d² = bc·cos A. Llamando AM = m = b·cos A a la proyección ortogonal del lado b sobre c se tiene ahora 4d² = mc. El segmento 2d es la media geométrica de los segmentos m y c que es fácil de construir.

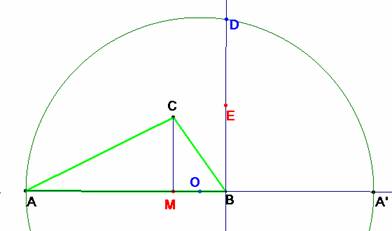
Se toma m=BA’ a continuación de c y en la circunferencia que tiene por diámetro c + m el segmento BD, perpendicular a a AA’ es igual a 2d. Si E es su punto medio tenemos d= BE.

Si el ángulo A es obtuso, su coseno es negativo así como b²+c²- a² y no existe d. (Si es recto vale 0).