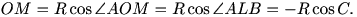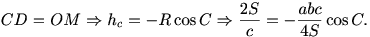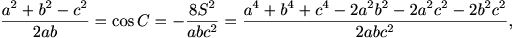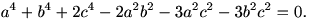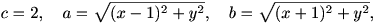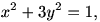Solución de Francisco Javier García Capitán
|
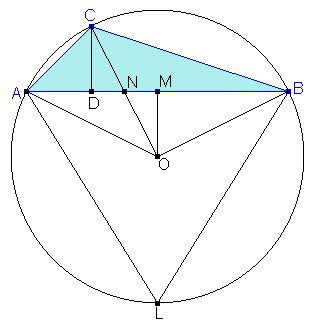
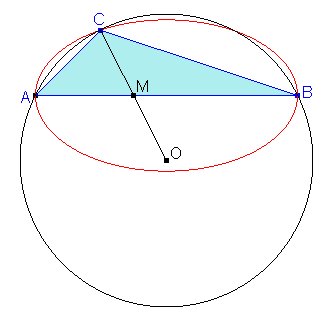
Si consideramos la figura, un triángulo ABC con AB fijo que cumpla la propiedad tendrá una altura CD igual a la distancia OM del circuncentro al lado AB.
Sean, como es habitual, R, s y S el radio de la circunferencia circunscrita, el perímetro y el área del triángulo ABC. Entonces,
Entonces, De aquí obtenemos obteniendo la relación Recordemos que el lado AB es fijo, por lo que podemos considerar A=(-1,0), B=(1,0) y C=(x,y). Entonces tendremos: y puede verse sin dificultad que al sustituir estos valores en la relación anterior obtenemos la ecuación que corresponde a una elipse con eje mayor el segmento AB. Dos vértices de la elipse serían entonces los puntos A y B, y los otros dos son los baricentros de los triángulos equiláteros construidos sobre AB.
|