Para el aula
Propuesto por José María Pedret. Ingeniero Naval. (Esplugas de Llobregat, Barcelona)
Problema 416
En un triángulo ABC se sabe que la base es fija y que el punto medio de CO está en AB, siendo O el circuncentro. Hallar el lugar geométrico del vértice C.
Resuelto por JULIÁN SANTAMARÍA TOBAR profesor de Dibujo del IES La Serna de Fenlabrada
|
|
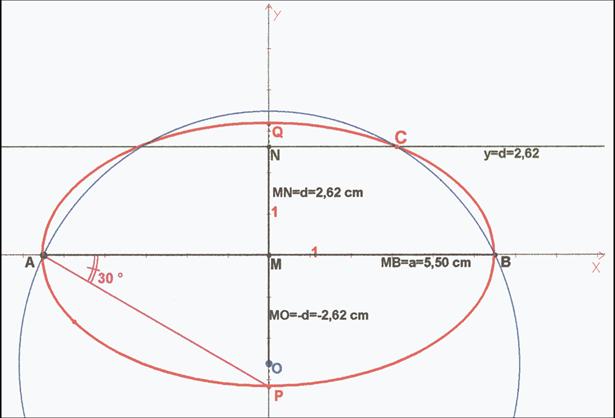
Sea M el punto medio del segmentoAB
de longitud 2a y se hace coincidir con el centro de coordenadas.
La circunferencia
circunscrita pasa por los vértices A y B. El centro O está en la mediatriz de
AB: en el eje “y” a una distancia “d” de la recta AB. Su ecuación es la
siguiente:
x2 + (y
+ d)2 = d2 + a2
Si el punto medio de CO
está en AB, el lugar geométrico de los puntos simétricos de O respecto de cada
uno de los puntos de la recta AB forma una paralela a AB separada la distancia
d. En esta recta está el vértice C. La ecuación de la recta es la siguiente:
y=d
Teniendo en cuenta que la
distancia d es variable, la intersección de la recta y la circunferencia da
como resultado el lugar geométrico pedido. Sustituyendo d por y en ecuación de
la circunferencia resulta:
x2 + (y + y)2 = y2
+ a2 Þ x2 + 4y2
= y2 + a2 Þ x2 + 3y2 -
a2 = 0
Por lo tanto el lugar
geométrico pedido es una elipse y su cento es el punto medio de AB.
Los vértices del eje
mayor: para y = 0; x = ± a. Luego los vértices son
A y B
Los vértices del eje
menor: para x = 0; y = ± a / Ö3
El ángulo MAP del
triángulo rectángulo formado por los semiejes será:
Arc tg [(a / Ö3)/ a] = Arc tg (1 / Ö3) = 30º
En definitiva, el lugar
geométrico es una elipse cuyo eje mayor es AB y para dibujar el eje menor se trazan
por el punto A las rectas que formen 30º con el eje AB y cortarán a la
mediatriz de AB en los vértices P y Q del eje menor.