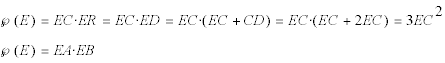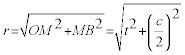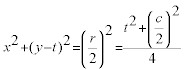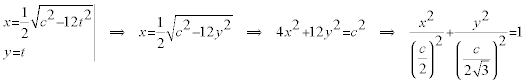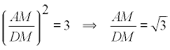|
Para el aula. Propuesto por José María Pedret. Ingeniero Naval. (Esplugas de Llobregat, Barcelona) Problema 416. En un triángulo ABC se sabe que la base es fija y que el punto medio de CO está en AB, siendo O el circuncentro. Hallar el lugar geométrico del vértice C. Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de noviembre de 2007) |
|
INTRODUCCIÓN |
|
|
Aprovechamos este enunciado para presentar tres soluciones
En el caso de regla y compás, está claro que para buscar la solución hay que tener una idea de por donde va. Como el lugar buscado resulta ser una elipse, buscamos un círculo conveniente que se transforme en ella por medio de una afinidad sencilla. El método a desarrollar puede llegar a ser bastante complejo, aunque utilice herramientas fáciles; las más “complicadas” son el arco capaz, la potencia respecto a un círculo y la media geométrica de dos segmentos en prolongación. En el caso analítico, basta con encontrar la intersección de una recta y un círculo que dependan de un parámetro, automáticamente obtenemos la ecuación en paramétricas y de ahí la ecuación implícita ( o explícita si se prefiere). En este enunciado el procedimiento analítico es extremadamente simple y elegante. CABRI II PLUS ver. 1.4 da la solución más vistosa y es extremadamente simple (y dinámica). Construyendo simplemente el enunciado, como se especifica al principio de la construcción con regla y compás, y pidiendo a CABRI el lugar geométrico del punto C al variar el punto O, obtenemos que el lugar es una elipse y su ecuación que coincide con las anteriores. |
|
SOLUCIÓN CON REGLA Y COMPÁS |
|
|
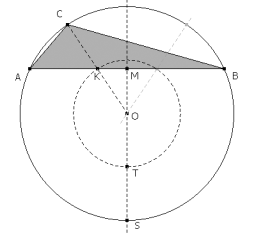
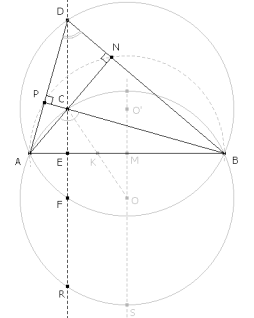
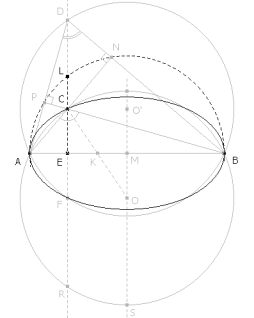
DIBUJO DE UNO DE LOS TRIÁNGULOS QUE CUMPLE CON EL ENUNCIADO Fijados A y B , consideremos un círculo circunscrito cualquiera. Para ello, dibujamos la mediatriz de AB y sobre la misma tomamos un punto variable O. Trazamos el círculo de centro O y que pasa por A.
Sea K el punto medio de OC. Como A, B, C están sobre el círculo circunscrito se cumple
es decir, K está sobre el círculo de centro O y radio la mitad del radio del círculo circunscrito. Trazado este círculo, imponemos la segunda condición del enunciado (K está sobre AB ). K está en la intersección del círculo anterior y la recta AB. C se encuentra en la intersección de OK con el círculo circunscrito. Podemos observar que existe otro vértice C simétrico al anterior respecto al la mediatriz de AB, ya que hay dos intersecciones entre el círculo de K y la recta AB.
Si nos fijamos en M, el punto medio de AB, tenemos además que
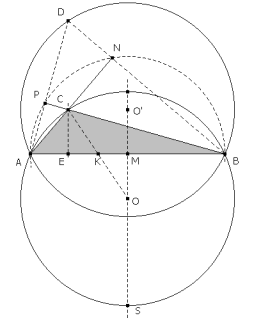
TRAZAMOS UN CÍRCULO AUXILIAR
Con diámetro AB trazamos un semicírculo por la parte opuesta a O. El lado BC corta a este semicírculo en N y el lado AC lo corta en P. Definimos el punto D como la intersección de BN con AP. Trazamos el círculo circunscrito al triángulo ABD que tiene su centro en O’. EL CÍRCULO CIRCUNSCRITO AL TRIÁNGULO ABD ES SIMÉTRICO AL CÍRCULO CIRCUNSCRITO AL TRIÁNGULO ABC RESPECTO LA RECTA AB.
Hallemos el valor del ángulo ∠ADB observando el cuadrilátero PCND.
pero ∠π-C es el ángulo suplementario de C y por tanto es el ángulo del arco capaz que define el círculo circunscrito al triángulo ABC . Por ejemplo, en la figura 4, ∠ASB=∠π-C. Lo anterior indica que los dos círculos tienen el mismo arco capaz con el segmento AB y por lo tanto son simétricas respecto a dicho segmento. Podemos pues deducir que
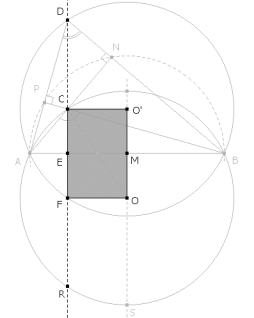
D ESTÁ ALINEADO CON C, E, F
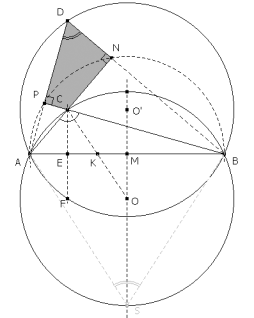
AC es perpendicular a BD y BC es perpendicular a AD, entonces C es el ortocentro del triángulo ABD. La perpendicular a AB desde el vértice D ha de pasar por el ortocentro C y como CE también es perpendicular a AB deducimos que D, C, E, F están alineados. F es la intersección de CE con el círculo circunscrito al triángulo ABD y R es la intersección de CE con el círculo circunscrito al triángulo ABC. C ES EL PUNTO MEDIO DE AF La igualdad deducida anteriormente de CE, EF, MO, MO’ nos permite deducir que el cuadrilátero CFOO’ es un rectángulo.
Entonces O’C es perpendicular a AF y por tanto C es el punto medio de DF, esto nos permite escribir
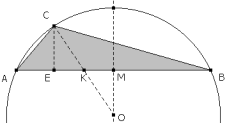
EL PUNTO E Y EL PUNTO AUXILIAR L La potencia de E respecto del círculo circunscrito al triángulo ABC se puede expresar de dos maneras
pero
si consideramos el semicírculo de diámetro AB y el punto L de intersección de la perpendicular por E a AB y el semicírculo, tenemos que
Este resultado con la ecuación anterior
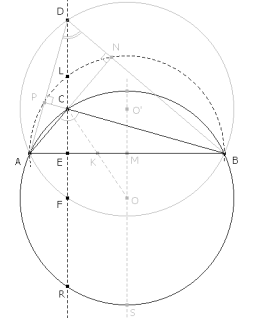
EL LUGAR GEOMÉTRICO BUSCADO
Al desplazar O sobre la mediatriz de AB, el punto L recorre el semicírculo de diámetro AB y por lo tanto el punto C recorre la transformada afín del círculo según
Es decir
|
|
SOLUCIÓN ANALÍTICA |
|
|
EL ENUNCIADO Recordemos de la solución con regla y compás que K está sobre el círculo de centro O y radio la mitad del radio del círculo circunscrito
Tomamos un sistema de coordenadas con origen en M, con AB eje de abscisas y la mediatriz de AB como eje de ordenadas. Como O es variable sobre el eje de ordenadas
donde t es un parámetro variable y c = AB. El radio del círculo circunscrito es
La ecuación del círculo del radio mitad del círculo circunscrito y con centro en O es
La ecuación de la recta AB es
la intersección de círculo y recta es
pero
que es la ecuación en paramétricas de una elipse en la que eliminando el parámetro obtenemos
y como AB = c , concluimos que
|
|
SOLUCIÓN DINÁMICA CABRI II PLUS ver. 1.4 |
|
|
DIBUJO DE UNO DE LOS TRIÁNGULOS QUE CUMPLE CON EL ENUNCIADO Repetimos la construcción de una posición del vértice C (ver la solución con regla y compás)
puede deplazar A y O
puede deplazar A y O Si no está instaldo, descargar Cabri II Plus plug-in. Nos da una elipse de eje mayor AB. Para ver el eje menor buscamos la relación entre ejes por medio de CABRI y su herramienta distancia o longitud
Aunque aquí no es necesario, añadimos el círculo de diámetro AB par poner de manifiesto que la elipse obtenida es la transformada de dicho círculo. |