Problemea 416

En un triangle  sabem que la base és fixa i que el punt mig de  pertany a  essent O el circumcentre. Determineu el lloc geomètric del punt C.

Propuesto por José María Pedret. Ingeniero Naval. (Esplugas de Llobregat, Barcelona)

Solució de Ricard Peiró:

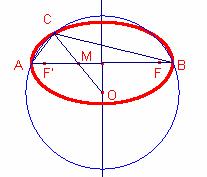Siga el segment  amb les següents coordenades cartesianes , .

El circumcentre O del triangle pertany a la mediatriu del segment .

Siguen les seues coordenades , suposem que .

Aleshores l’ordenada de C és major que zero.

El radi de la circumferència circumscrita al triangle és .

L’equació de la circumferència circumscrita al triangle és:

. Simplificant:

.

Les coordenades de C són:

Siga M el punt mig del segment .

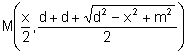
Com que M pertany al segment , la seua ordenada és zero. Aleshores:

. Resolent l’equació en la incògnita d:

.

Aleshores les coordenades de C són:

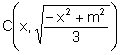
Vegem quin lloc geomètric recorre C:

Siga . Elevant al quadrat i simplificant:

 que és una el·lipse. Determinem els seus elements:

.

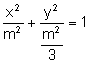Els semieixos són , ,  .

L’excentricitat de l’el·lipse és,  i els focus , .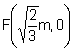

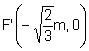Aleshores el lloc geomètric és una el·lipse de centre en punt mig del segment  que té per semiexos , .

Nota si  el resultat seria l’altra semiel·lipse.