Problemea 416

En un triángulo ABC se sabe que la base es fija y que el punto medio de CO está en AB, siendo O el circuncentro. Hallar el lugar geométrico del vértice C.

Pedret, J.M. (2007) Comunicación personal

Solución de Ricard Peiró:

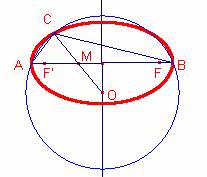Sea el segmento  con las siguientes coordenadas cartesianas , .

El circumcentro O del triángulo pertenece a la mediatriz del segmento .

Las coordenadas del circuncentro , supongamos que .

Entonces la ordenada de C es mayor que cero.

El radio de la circunferencia circunscrita al triángulo es .

La ecuación de la circunferencia circunscrita al triángulo es:

. Simplificando:

.

Les coordenadas de C son:

Sea M el punto medio del segmento .

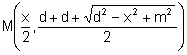
Como M pertenece al segmento , su ordenada es cero. Entonces:

. Resolviendo la ecuación con la incógnita d:

.

Entonces las coordenadas de C son:

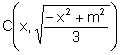
Determinemos el lugar geométrico que recorre C:

Sea . Elevando al cuadrado y simplificando:

 que es una elipse. Determinemos sus elementos:

.

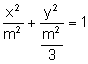Los semiejes son , ,  .

La excentricidad de la elipse es,  y los focos , .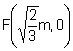

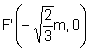Entonces el lugar geométrico es una elipse de centro en punto medio del segmento  que tiene por semiejes , .

Nota si  el resultado seria la otra semielipse.