Problema 416. (Propuesto por J. María Pedret,
Ingeniero Naval, Esplugas de Llobregat,
Barcelona).
En un triángulo ABC se sabe que su base AB es fija y que el punto medio de CO está en AB, siendo O el circuncentro del triángulo. Hallar el lugar geométrico del
vértice C.
Resolución: (Vicente Vicario García, I.E.S.
El Sur, Huelva).
Usaremos la geometría de coordenadas
y supondremos, sin pérdida de generalidad, que 
y 
. El punto 
será el del lugar
geométrico buscado (
para que exista el triángulo).
Determinemos las ecuaciones de las rectas mediatrices de los segmentos AC y CB para poder así calcular las coordenadas del circuncentro del triángulo ABC.
Mediatriz de AC 
Mediatriz de BC 
Las coordenadas del circuncentro O vendrán dadas por la solución del sistema de ecuaciones lineales relativas a las mediatrices anteriores:
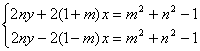
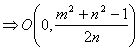
Imponiendo ahora la condición de que el punto medio M de CO pertenezca al lado AB del triángulo, es decir, anulando la segunda de las coordenadas del punto M, tenemos que
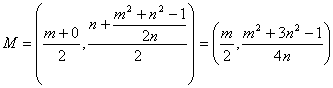
Entonces, las coordenadas del punto C buscado son 
que podemos expresar
en forma paramétrica dependiente del parámetro n:
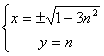
Eliminando este parámetro n entre las dos ecuaciones tenemos finalmente
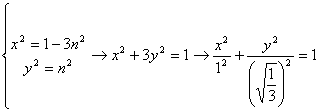
que es la ecuación reducida de una elipse centrada en el origen y no
girada de semiejes 
.
Finalmente,
observando la medida del lado
del triángulo ABC, y
tras considerar la correspondiente figura homotética de
la elipse anterior , con centro de homotecia el origen
de coordenadas y razón de homotecia 
, el lugar geométrico pedido será: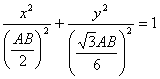 
que es la ecuación reducida de una elipse centrada en el origen y no
girada de semiejes 
.