Solución de Francisco Javier García Capitán
Sean D, E, F los pies de las bisectrices interiores trazadas
por A, B y C, respectivamente:
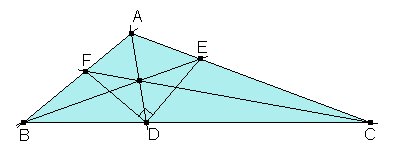
Por ser BD:DC = AB:AC = c:b, las coordenadas baricentricas de D son (0:b:c), y de forma análoga, las de E son (a:0:c) y las de F son (a:b:0). También podemos obtener estas coordenadas a partir de que el incentro es I = (a:b:c).
Que el ángulo EDF es recto lo podemos expresar diciendo que F está en la perpendicular a DE trazada por D.
Usamos Mathematica y el fichero Baricentricas.nb:

Ahora hacemos
![]()
Con esta compacta instrucción hemos obtenido factorizada la expresión que debe anularse cuando el punto F esté sobre la perpendicular a DE trazada por D.
Entonces tenemos:
![]()