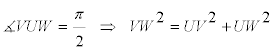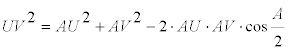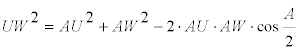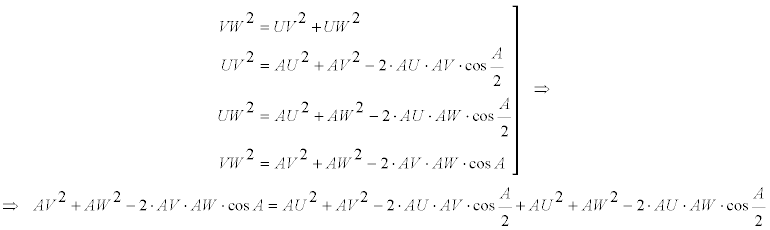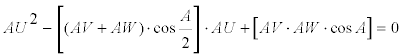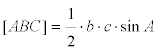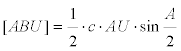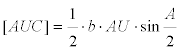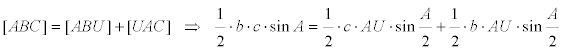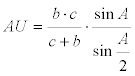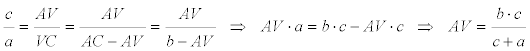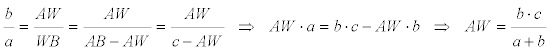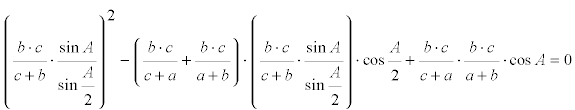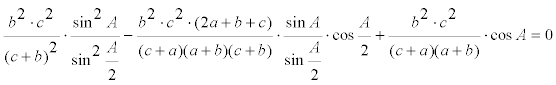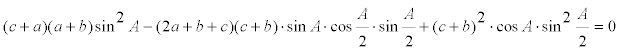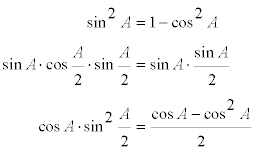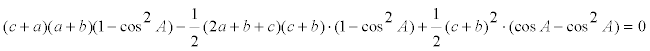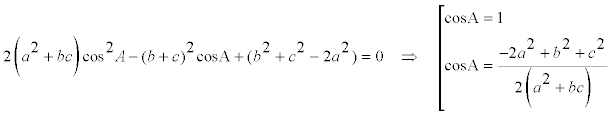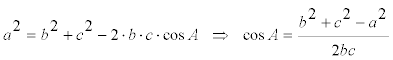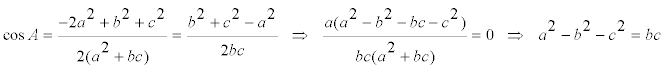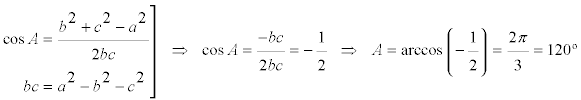De investigación. Propuesto por Vicente Vicario García, profesor del I.E.S. El SUR, Huelva

Problema 417

Demostrar que si en un triángulo ABC, el triángulo formado por los pies de sus bisectrices interiores es rectángulo, entonces dicho triángulo tiene un ángulo de 120º.

Nota: Este problema surge como teorema recíproco al teorema establecido en el problema 9 de esta misma revista. Dicho problema se enunció así: “Demostrar que si en un triángulo ABC un ángulo es de 120º, el triángulo formado por los pies de las bisectrices interiores es rectángulo.” (G. Sánchez Vázquez. Métodos gráficos de resolución de problemas geométricos. Pág 16. SAEM THALES. Sevilla. 1996.)

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (2 de noviembre de 2007)

SOLUCIÓN

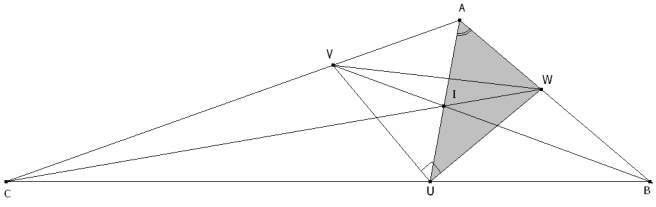
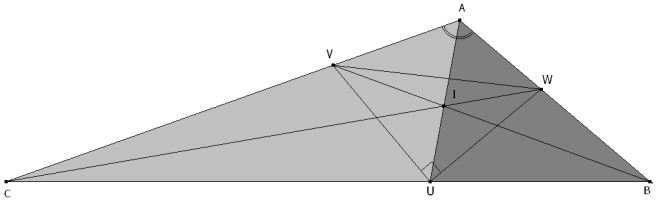
DIBUJO DEL ENUNCIADO

figura 1

Como siempre

y nombramos los pies de las bisectrices como

U el pie de la bisectriz de A

V el pie de la bisectriz de B

W el pie de la bisectriz de C

A partir de aquí usaremos todas las relaciones posibles que podamos obtener de los distintos triángulos de la figura; pero siempre con el ángulo A (o su mitad).

EL TEOREMA DE PITÁGORAS EN EL TRIÁNGULO UVW

figura 2

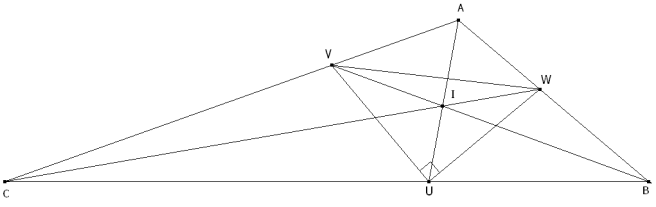
Como el enunciado nos dice que dos bisectrices interiores forman ángulo recto supondremos que el ángulo recto es el opuesto a A

  [1]

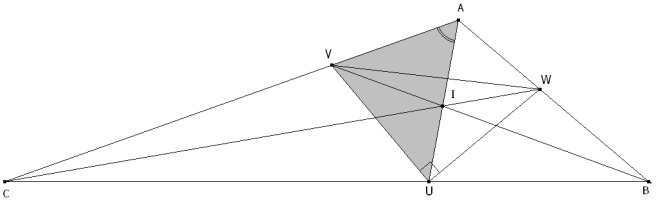
Debemos hallar expresiones para UV, UW y VW

EL TEOREMA DEL COSENO EN EL TRIÁNGULO AUV

figura 3

  [2]

EL TEOREMA DEL COSENO EN EL TRIÁNGULO AUW

figura 4

  [3]

EL TEOREMA DEL COSENO EN EL TRIÁNGULO AVW

figura 5

  [4]

REUNIÓN DE LAS ECUACIONES [1], [2], [3] Y [4]

Sustituyendo [2] , [3] y [4] en [1]

que simplificada queda como

  [5]

Debemos hallar expresiones para AU, AV y AW

LA EXPRESIÓN DE AU

figura 6

El área del triángulo ABC

  [6]

El área del triángulo ABU

  [7]

El área del triángulo AUC

  [8]

Combinando ahora [6], [7] y [8]

de donde podemos despejar AU

  [9]

LA EXPRESIÓN DE AV

Por el teorema de la bisectriz BV en el triángulo ABC

  [10]

LA EXPRESIÓN DE AW

Por el teorema de la bisectriz CV en el triángulo ABC

  [11]

EL ÁNGULO A

Sustituyendo [9], [10] y [11] en [5]

  [12]

desarrollando la ecuación

  [13]

eliminando denominadores y factores distintos de cero no necesarios

  [14]

donde teniendo en cuenta las igualdades trigonométricas

nos queda

  [15]

y ordenando en potencias del coseno de A

  [16]

donde no consideramos la primera solución; pero el teorema del coseno en ABC también nos da

  [17]

igualando los dos cosenos ([16] y [17])

  [18]

y retomando de nuevo [16] con el valor de [18]

que era lo que queríamos demostrar.