De investigación

Propuesto por Vicente Vicario García, profesor del I.E.S. El SUR, Huelva

Problema 417.- Demostrar que si en un triángulo ABC, el triángulo formado por los pies de sus bisectrices interiores es rectángulo, entonces dicho triángulo tiene un ángulo de 120º.

Nota: Este problema surge como teorema recíproco al teorema establecido en el problema 9 de esta misma revista. Dicho problema se enunció así: “Demostrar que si en un triángulo ABC un ángulo es de 120º, el triángulo formado por los pies de las bisectrices interiores es rectángulo”. (G. Sánchez Vázquez. Métodos gráficos de resolución de problemas geométricos. Pág 16. SAEM THALES. Sevilla. 1996.)

Vicario, V, (2007): Comunicación personal.

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca

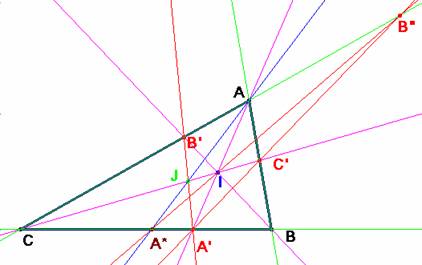
Sea ABC un triángulo; AA’, BB’ y CC’ tres cevianas concurrentes en I. Tomamos J=A’B’·CC’, A*=AJ·BC y B”=A*I·AC. Las cevianas de AA’C concurrentes en J (AA*, A’B’ y CI) determinan que la cuaterna (CAB’B”) sea armónica. Por igual razón las cevianas de ABC concurrentes en I determinan que B”=A’C’·AC, pues el cuarto armónico de tres puntos es único (esto es, las rectas AC, A*I y A’C’ son concurrentes).

Si A’B’ y A’C’ son perpendiculares, son las bisectrices interior y exterior del ángulo AA’C. Si además AA’ y CC’ son bisectrices interiores de ABC, el punto C’ es uno de los excentros del triángulo AA’C, y por tanto, son iguales los tres ángulos, cuya suma es un llano, CAA’, A’AB y BAB” de lo cual se concluye que el ángulo CAB mide 120º.