Problema 417

“Demostrar que si en un triángulo ABC, el triángulo formado por los pies de sus bisectrices interiores es rectángulo, entonces dicho triángulo tiene un ángulo de 120º ”.

Nota: Este problema surge como teorema recíproco al teorema establecido en el problema 9 de esta misma revista. Dicho problema se enunció así: “Demostrar que si en un triángulo ABC un ángulo es de 120º, el triángulo formado por los pies de las bisectrices interiores es rectángulo”. (G. Sánchez Vázquez. Métodos gráficos de resolución de problemas geométricos. Pág 16. SAEM THALES. Sevilla. 1996.)

Vicario, V. (2007): Comunicación personal.

Resolución: (Vicente Vicario García, Huelva)

Emplearemos la notación usual de la geometría del triángulo. Consideremos un triángulo ABC y las bisectrices interiores de sus ángulos A, B, C que intersecan los lados opuestos en los puntos D, E, F respectivamente. Inicialmente demostraremos un lema.

Lema: “La longitud de la bisectriz interior AD de un triángulo ABC viene dada por las siguientes igualdades:

”. [1]

Para la demostración del lema denotemos y apliquemos el teorema de la bisectriz interior, con lo que resulta

;

Aplicando ahora el teorema de los cosenos al triángulo ABD y utilizando la expresión de en función de los lados del triángulo tenemos

y después de simplificar resulta la primera igualdad del lema. Para demostrar la segunda basta aplicar la identidad trigonométrica y la expresión de en función de los lados del triángulo. ■

Para la demostración general, aplicando el teorema de los cosenos a los triángulos ADE y ADF, resulta

[2]

Aplicando el teorema de los cosenos al triángulo AEF tenemos

[3]

Si suponemos ahora que el triángulo formado por los pies de las bisectrices interiores es rectángulo, aplicando el teorema de Pitágoras, y sin pérdida de generalidad las expresiones [2] y [3] tenemos

que después de simplificar resulta

[4]

Utilizando el teorema de la bisectriz interior, el lema, y teniendo en cuenta la identidad trigonométrica del coseno del ángulo doble, resulta entonces

;

e incorporando estos valores en la expresión [4] tenemos

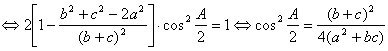
y esta última relación nos lleva, finalmente a

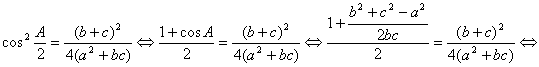
Comparando esta última expresión obtenida con la que resulta del teorema de los cosenos aplicado al triángulo ABC, () deducimos que , y por tanto, .