Solución de Francisco Javier García Capitán
|
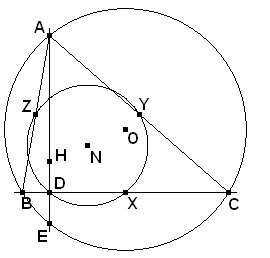
Si consideramos un punto A sobre la circunferencia G y trazamos la altura AH, sabemos que cortará a de nuevo a G en un punto E simétrico de H respecto del lado BC. Esto determina la recta BC, y considerando la intersección con G, a los otros dos vértices B y C. Los puntos medios de estos triángulos estarán en las circunferencias de los nueve puntos de cada uno de ellos, pero observemos que todas estas circunferencias coinciden en una sola, ya que su centro N es el punto medio de O y H, que son fijos, y el radio la mitad que el de G. Así, el lugar geométrico pedido es la circunferencia con centro N, punto medio de O y H y radio la mitad que el de G . |
 |