De investigación
Propuesto por José María Pedret. Ingeniero Naval. (Esplugas de Llobregat, Barcelona)
Problema 418
En un plano cualquiera, se dan:
* un círculo Γ de centro O,
* un punto fijo H.
En Γ se inscriben triángulos variables ABC, cuyo ortocentro es H.
* Hallar el lugar geométrico del punto medio de uno de los lados del triángulo.
* Caracterizar dicho lugar geométrico.
Resuelto por JULIÁN SANTAMARÍA TOBAR profesor de
Dibujo del IES
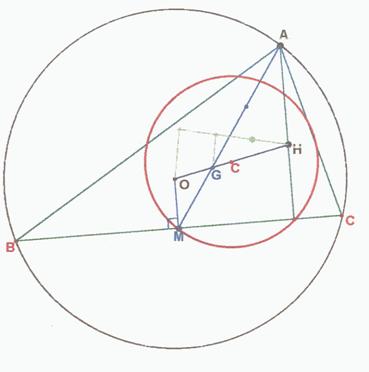
Dada la circunferencia circunscrita de centro O y el ortocentro H, se puede hallar el baricentro G porque “el
baricentro de un triángulo está alineado con el ortocentro
y el circuncentro y a doble distancia del primero que
del segundo. La recta que contiene a estos puntos se llama recta de Euler. (Problema nº7)”
Al tomar un punto cualquiera A de la circunferencia, la relación que tiene el vértice A con el punto medio M del lado opuesto respecto al punto fijo G es un homotecia de razón -1/2. Si el punto A puede tomar cualquier posición de la circunferencia el lugar geométrico de los puntos medios M de los posibles lados opuestos es una circunferencia homotética de razón -1/2 de la circunferencia circunscrita.
La homotecia del centro O con respecto al centro de
homotecia G resulta C. Situación del centro C: GC = OG/2; y OG = OH/3 Þ OC =
OH/3 +
(OH/3)/2 = OH/2
Caracterizar
dicho lugar geométrico:
La circunferencia que tiene como centro el punto medio C
entre O y H y su radio es la mitad de la circunscrita es la circunferencia de Euler, Feuerbach o de los nueve
puntos (ver problemas 8, 12,…)