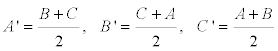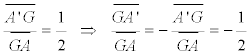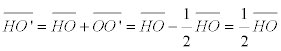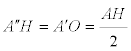En un plano cualquiera, se dan

• un círculo Γ de centro O,
• un punto fijo H.

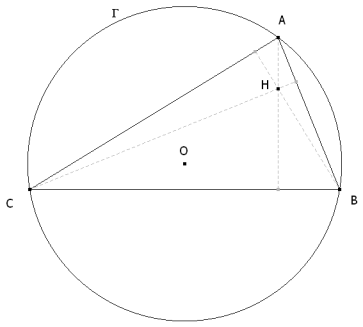
En Γ, se inscriben triángulos variables ABC, cuyo ortocentro es H.

• Hallar el lugar geométrico del punto medio de uno de los lados del triángulo.
• Caracterizar dicho lugar geométrico.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (16 de noviembre de 2007)

SOLUCIÓN

figura 1

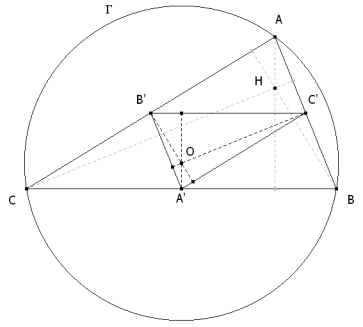
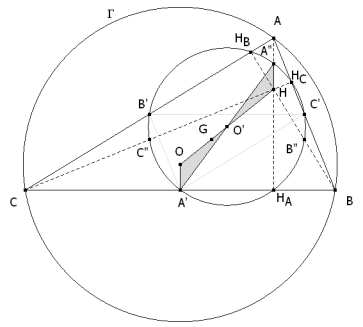
ABC Y EL TRIÁNGULO A'B'C' DE VÉRTICES LOS PUNTOS MEDIOS DE LOS LADOS DE ABC SON HOMOTÉTICOS

Dibujamos uno cualquiera de los triángulos ABC que cumple con el enunciado. Los puntos medios de ABC son

figura 2

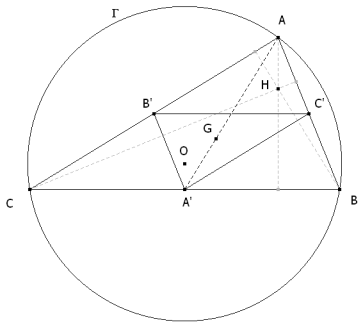
Dibujamos ahora el triángulo A’B‘C’. Observemos la mediana AA’. Sabemos que si G es el baricentro de ABC

y análogas relaciones obtendríamos para B’ y C’; deducimos que

Los triángulos ABC y A’B’C’ son homotéticos en una homotecia de centro G y razón -½.

EL CIRCUNCENTRO DEL TRIÁNGULO ABC ES EL ORTOCENTRO DEL TRIÁNGULO A’B’C’

figura 3

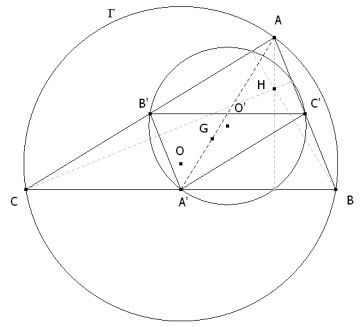
Sabemos que el circuncentro O es el punto de concurrencia de las mediatrices del triángulo ABC. Las mediatrices como perpendiculares a los lados en el punto medio son las alturas del triángulo A’B’C’ ya que los puntos medios de los lados de ABC son los vértices de A’B’C’ y además, al ser los dos triángulos homotéticos sus lados son paralelos y por lo tanto las mediatrices del primero también son perpendiculares a los lados del segundo; entonces, las mediatrices de ABC son las alturas de A’B’C’ y por lo tanto O es el punto de concurrencia de las alturas de A’B’C’ y en consecuencia su ortocentro. Deducimos que

El homotético del ortocentro H en la homotecia de centro G y razón -½ es el circuncentro O.

y por lo tanto G, H, O, O’ están alineados.

EL LUGAR DE LOS PUNTOS MEDIOS DE LOS LADOS DEL TRIÁNGULO ABC ES UN CÍRCULO

Como los vértices A, B, C se desplazan a lo largo de Γ, los puntos A’, B’, C’ recorren el círculo homotético a Γ con centro en O’ (homotético de O en la homotecia de centro G y razón -½) y radio la mitad del de Γ.

figura 4

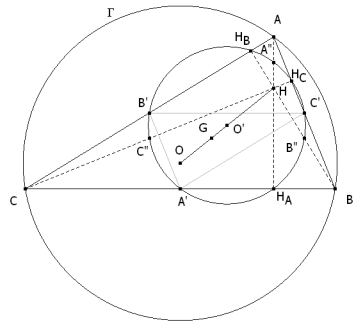
EL CÍRCULO HALLADO ES EL CÍRCULO DE NUEVE PUNTOS ( DE EULER O DE FEUERBACH )

El círculo pasa por los puntos medios de los lados. Comprobemos que pasa también por A”, B”, C” los puntos medios de AH, BH y CH y por H_A, H_B, H_C los pies de las alturas del triángulo ABC

figura 5

En la homotecia de centro G y razón -½

y como

entonces O’ es el punto medio de OH, lo que nos permite trazar la siguiente figura

figura 6

que nos permite ver que

por lo tanto A” es el punto medio de AH.

figura 7

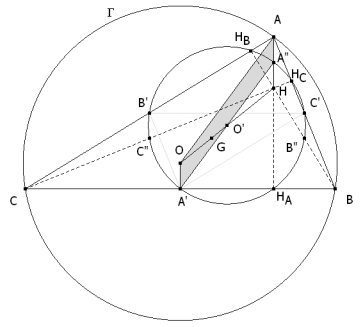
AO y A’O’ son paralelas por ser homotéticas en la homotecia de centro G y razón -½; y como A’O es igual a AA”=AH y además son paralelos, OA’A”A es un paralelogramo y por tanto A’, O’, A” están alineados con lo que A’A” es diámetro del círculo de centro O’ y entonces como el ángulo ∠AH_AA’ es recto, H_A está sobre el círculo de diámetro AA’.

CONCLUSIÓN

El lugar geométrico de los puntos medios de los lados de los triángulos ABC inscritos a un círculo dado Γ de centro O y de ortocentro fijo H, es el círculo de centro O’ punto medio de OH y radio mitad del círculo dado.

El círculo anterior es el círculo de nueve puntos, llamado también círculo de Euler o círculo de Feuerbach.