De investigación.

Propuesto por José María Pedret. Ingeniero Naval. (Esplugas de Llobregat, Barcelona).

Problema 418.-

En un plano cualquiera, se dan:

    *   un círculo Γ de centro O,

    *   un punto fijo  H.

En Γ se inscriben triángulos variables ABC, cuyo ortocentro es H.

    *   Hallar el lugar geométrico del punto medio de uno de los lados del triángulo.

* Caracterizar dicho lugar geométrico. 

Pedret, J.M. (2007): Comunicación personal.

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca.

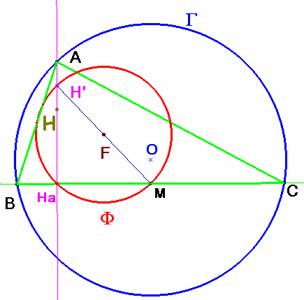
Con ortocentro y circuncentro fijos, también es fijo el centro F de la circunferencia de los nueve puntos F, que es el punto medio de OH. En esta circunferencia se encuentran, entre otros, los puntos medios de los lados de los triángulos buscados.

Para construir esos triángulos con los datos que tenemos, trazo la circunferencia de los nueve puntos y elijo un punto cualquiera A sobre G, trazo la recta AH, una altura. Alcanzará a la circunferencia de Euler en dos puntos, el más cercano a A, H’ es el punto medio de AH, mientras que el otro H_a, es el pie de esa altura. La perpendicular por este punto a AH encuentra a la circunscrita en los puntos B y C que completan el triángulo. Su punto medio es M. Al variar A sobre G, también lo hace M. Buscamos el lugar geométrico descrito por éste último.

La correspondencia que asocia a un punto A de G, un punto M de F es biunívoca. Ya hemos visto en un sentido. Si ahora tomo un punto M sobre F, H’ es el punto diametralmente opuesto en la circunferencia de Euler, y A es el simétrico de H respecto a él. Por todo ello el lugar geométrico de los puntos medios de los lados es la circunferencia de los nueve puntos de todos esos triángulos.