Solución de Francisco Javier García Capitán
|
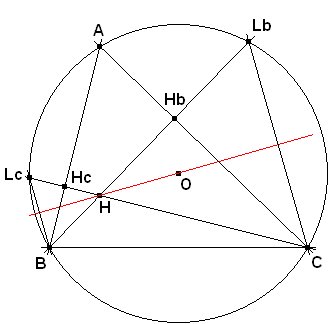
Prolongamos las alturas BHb y CHc hasta cortar a la circunferencia
circunscrita en Lb y Lc, respectivamente. Los triángulos BHLc y CHLb, que siempre son isósceles
en B y C respectivamente, aquí son equiláteros, por ser
A=60º. Entonces, la bisectriz del ángulo H es mediatriz
de los lados BLc y CLb, cuerdas de la circunferencia circunscrita, y
la mediatriz de cualquier cuerda de una |
 |