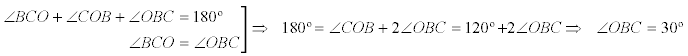|
De investigación. Propuesto por Francisco Javier García Capitán, profesor del IES Álvarez Cubero (Priego de Córdoba) Problema 419. M1046. En el triángulo acutángulo ABC el ángulo A es 60º. Demostrar que una de las bisectrices del ángulo formado por las dos alturas trazadas desde los vértices B y C pasa por el circuncentro del triángulo. http://rs208.rapidshare.com/files/60756490/kvant.djvu ( página 107) Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (16 noviembre de 2007) |
|
SOLUCIÓN |
|
|
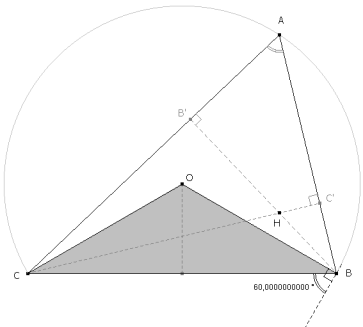
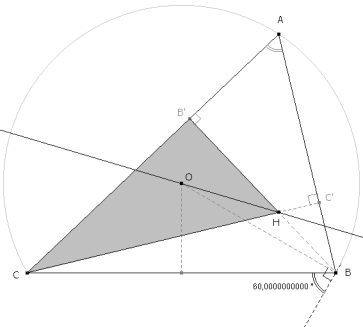
DIBUJAMOS EL ENUNCIADO
Fijamos la base BC y trazamos el arco capaz de 60º. Sobre el arco, el vértice A. En el centro del arco el ángulo es doble
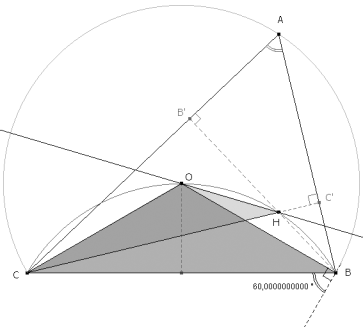
Pero siendo O el centro del círculo circunscrito al triángulo ABC,
lo que nos indica que el triángulo COB es isósceles y
OTROS ÁNGULOS
En el cuadrilátero AB’HC’
En el triángulo CHB por ángulos opuestos por el vértice
En el triángulo CHB’ , considerando ángulos suplementarios
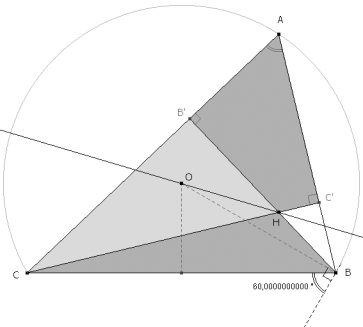
C, O, H, B ESTÁN EN EL MISMO ARCO CAPAZ
La igualdad de ángulos sobre la misma cuerda BC nos indica que O y H están sobre el mismo arco capaz. Entonces si fijamos en ese arco la cuerda CO
y de aquí volviendo al triángulo CHB’
y de aquí CONCLUSIÓN
de lo que deducimos que LA RECTA HO ES LA BISECTRIZ DEL ÁNGULO ∠CHB’
que es lo que queríamos demostrar. |