Problema 419
M1046. En el triángulo acutángulo ABC el ángulo A es 60º.
Demostrar
que una de las bisectrices del ángulo formado por las dos alturas trazadas
desde los
vértices B y C pasa por el circuncentro del
triángulo.
http://rs208.rapidshare.com/files/60756490/kvant.djvu
( página 107)
Solución de Ricard Peiró:
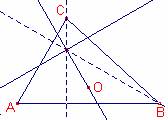
Sea el triángulo 
con las siguientes
coordenadas cartesianas:
, 
, 
. Notemos que 
.
La mediatriz al lado 
tiene ecuación: 
La mediatriz al lado 
tiene ecuación 
.
El circuncentro es la intersección de ambas
rectas.
Entonces tiene coordenadas: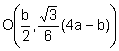 
.
La recta altura referida al lado tiene ecuación: 
La recta altura referida al lado tiene ecuación: 
Las ecuaciones de las rectas bisectrices son las soluciones de:
.
.
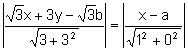
Veamos que 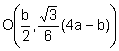pertenece a la recta 
:
, las coordenadas del punto O satisfacen la ecuación de la
recta .