De investigación.

Propuesto por Francisco Javier García Capitan, profesor del IES Álvarez Cubero (Priego de Córdoba).

Problema 419.-

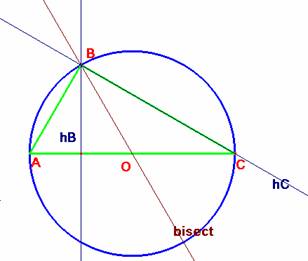
M1046. En el triángulo acutángulo ABC el ángulo A es 60º. Demostrar que una de las bisectrices del ángulo formado por las dos alturas trazadas desde los vértices B y C pasa por el circuncentro del triángulo.

http://rs208.rapidshare.com/files/60756490/kvant.djvu ( página 107)

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca.

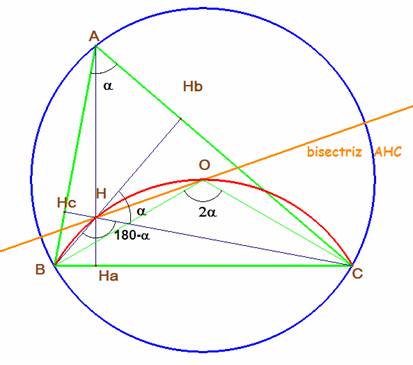
El cuadrilátero de vértices AH_cHH_b tiene dos ángulos rectos, por tanto los otros dos son suplementarios, como se indica en la figura para los ángulos de vértices A y H respectivamente. Las alturas desde B y C forman ángulos iguales al del triángulo en A y su suplementario.

Por el teorema del ángulo inscrito en una circunferencia el ángulo desigual del triángulo isósceles BOC es el doble del de A.

Cuando el ángulo BAC es de 60º los ángulos BHC y BOC son iguales, por tanto H y O están sobre el arco capaz de BC y amplitud 120º, y, en consecuencia, los ángulos OHC y OBC son iguales por abarcar el mismo arco. El ángulo OBC, en este caso, mide 30º, luego OHC=30º y como H_bHC =a = 60º, se tiene que la recta BO es la bisectriz de ese ángulo como se pretendía probar.

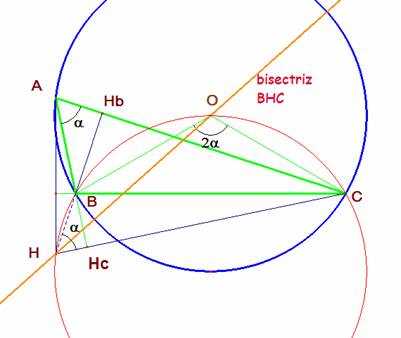
También es cierto el enunciado si el triángulo es obtusángulo.

En este caso el ortocentro es exterior al triángulo. El ángulo BHC es igual a a.

Cuando a=60º, en el cuadrilátero HBOC son suplementarios los ángulos en H y O por tanto también lo son el otro par de ángulos opuestos, de ahí los cuatro vértices están sobre una misma circunferencia. Como áng(OCB) =30º, también áng(BHO) =30º por abarcar el mismo arco y entonces áng(OHC) = a- 30º = 30º, resultando que HO es la bisectriz de BHC.

Cuando el triángulo es rectángulo, por ejemplo en B, también se cumple trivialmente