Problema 420: “Sean O,I,H el
circuncentro, incentro y ortocentro, respectivamente, de un triángulo
acutángulo ABC. Demostrar que si P es
un punto interior al triángulo y siendo 
la suma de las
distancias del punto P a los lados del triángulo, entonces, se tienen las
siguientes desigualdades
y
caracterizar cuándo se dan las igualdades”.
Resolución: (Vicente Vicario García, Huelva)
Utilizaremos la notación usual en la geometría del triángulo. Inicialmente deduciremos un lema y sus consecuencias.
Lema: “Con la notación habitual para un triángulo
sea A un ángulo del mismo, entonces
cosA es una raíz real de la
ecuación polinómica siguiente:
”.
Para
la demostración del lema consideremos las relaciones 
(teorema de los senos
generalizado) y 
(relacionada con el
incentro). Utilizando ahora las identidades trigonométricas del ángulo doble
Elevando al cuadrado y operando
se tiene
y después de manipulaciones algebraicas, llegamos a la relación que queremos
Claramente esta relación se cumple
también para 
y 
. De las relaciones de Cardano-Vieta entre las raíces y los
coeficientes deducimos las relaciones
[1]
Emplearemos
también la famosa desigualdad de Euler 
entre los radios de
las circunferencias circunscrita e inscrita a un triángulo, junto con la
desigualdad de Gerretsen† 
donde s es el semiperímetro, desigualdades que
se comentan en mi artículo sobre la caracterización del triángulo HIO en esta misma revista.
Obviamente
tenemos que 
. Determinemos ahora 
. Para ello bastaría con aplicar un famoso teorema de Carnot
que deduciremos. Evidentemente 
y denotemos 
como las distancias de
O a los lados 
del triángulo,
respectivamente. Por otra parte, los cuadriláteros 
,
,
son cíclicos y en virtud del teorema de Ptolomeo podemos
plantear las igualdades siguientes
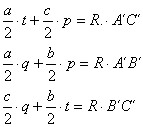[2]
Puesto que el área de un triángulo es el semiperímetro del mismo por el radio de su circunferencia inscrita, resulta también
[3]
Sumando ahora miembro a miembro las expresiones [2] y [3] resulta el teorema de Carnot, es decir
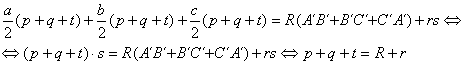
ya que obviamente 
puesto que 
son los puntos medios
de los lados del triángulo.
Ahora
es fácil demostrar que 
ya que 
debido a la
desigualdad de Euler . La igualdad se da sólo en el triángulo equilátero.
Pasemos
a determinar ahora 
. Para ello denotaremos por 
los pies de las
alturas trazadas desde los vértices 
respectivamente. Debido
a la semejanza de los triángulos 
y 
, aplicando el teorema de los senos generalizado y
expresiones trigonométricas básicas resulta
Ahora, puesto
que 
, entonces 
, y de forma análoga para las otras distancias. Entonces,
aplicando el lema, se tiene
y entonces podemos demostrar que 
ya que se tiene que
pero esta última desigualdad es
válida, ya que por la desigualdad de Gerretsen, si logramos demostrar que la
desigualdad, 
es cierta, entonces
también es cierta la desigualdad . Pero, efectivamente, esta última desigualdad es nuevamente
equivalente a la desigualdad de Euler . La igualdad de nuevo se da sólo en el triángulo equilátero.
.