Problema 421

Sea ABC un triángulo rectángulo en A, c<b <a. Trazamos la recta que
pasa por   el incentro I, y el circuncentro O, que corta a la prolongación de
AC, en   D, y AB, en E, respectivamente.
  Probar si es cierto o no :
  a) Que AD= a/2 si sólo si B =60
  b) Si F= AO y EC , entonces IF // AB si y sólo si B=60

Romero, J.B. (2007): Comunicación personal

Solución del director

a)

1.- Sea AD=a/2.

Sea ABC el triángulo rectángulo en A. Sea <ACB=C, <ABC=90-C.

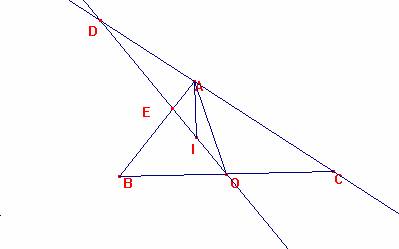
Sea AD=a/2=OB=R=AO, pues en el triángulo rectángulo el punto medio de la hipotenusa es el circuncentro y OB=OC=OA=R.

Luego el triángulo ADO es isósceles, <DAO=<ODA.

También el triángulo AOC es isósceles, por lo que <OAC=C.

Así, <OAD=180-C, y por ello, <AOI = <AOD = <ADO = C/2.

Además <ACI=C/2, por lo que el cuadrilátero AIOC es inscrito, y <IAO=<ICO=C/2.

Por otra parte, <IAO=<IAC-<OAC=45-C.

Así 45-C=C/2, luego 3C=90, C=30, C=60, cqd

2.- Sea el triángulo B=60 C=30 A=90.

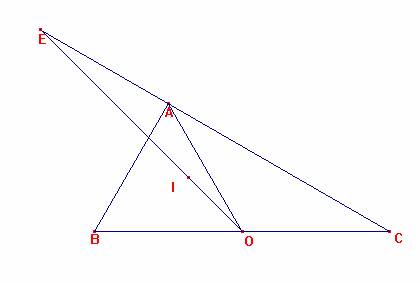
<OAC=<OCA=30, luego <AOC=120.

Por otra parte, <AIC=180-a/2-c/2=180-45-15=120.

Así, el cuadrilátero AIOC es inscrito, y <AOI=<COI=15.

Además, <OAE=180-<OAC=180-30=150.

Luego <AEO=180-<OAE-<AOI=180-150-15=15.

Así el triángulo AEO es isósceles, y AE=AO=OC=a/2, cqd

b) Si F= AO y EC , entonces IF // AB si y sólo si B=60

1.- Sea B=60.

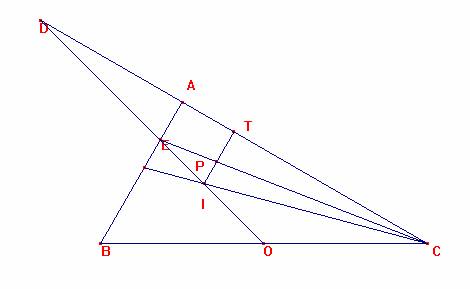
Tomemos sin pérdida de generalidad, c=1.

Es a=2, . Así, R=1, y .

Así, siendo T el punto de tangencia de AC con la inscrita, es:

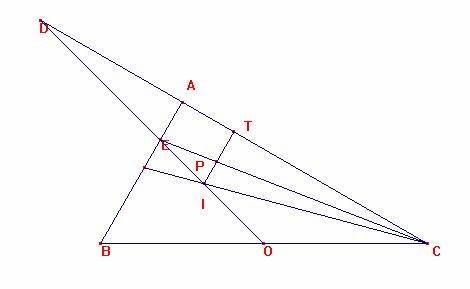
Los triángulos CIT y DIT son simétricos respecto a IT, pues en a) 2.-vimos que sus ángulos en C y D coincidían.

Luego DTI y DAE son semejantes.

Es:

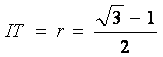, , luego

Por otra parte DA=1.

Así, tenemos que: AE/TI=DA/DT, de donde:.

Los triángulos CAE y CTP son semejantes. Luego:

Así, .

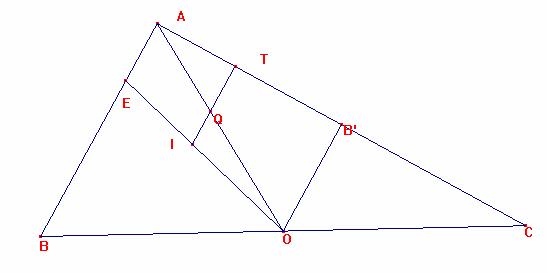
Tomemos ahora Q como punto de intersección de AO con IT .

Sea B’ el punto medio de AC.

Los triángulos ATQ y AB’O son semejantes.

,

, .

Así QT=PT, y ambos puntos coinciden con F, cqd.

2.- Supongamos ahora que en un triángulo rectángulo ABC con c<b<a, OI corta a AB en E y que CE, IT y AO, tienen un punto común.

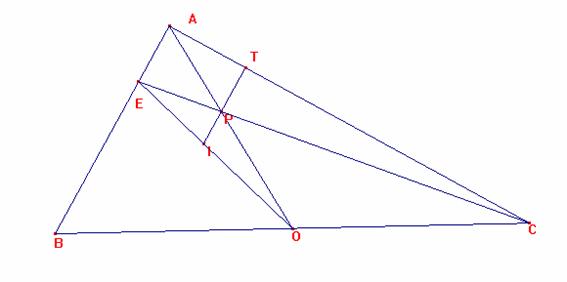
Sea OB=OC =OA=1.

Sea

Es

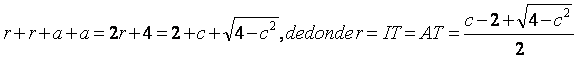
Sea B’ el punto medio de AC.

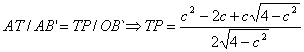
Así, es:

Además,

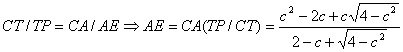
Por otra parte en el triángulo rectángulo APT tenemos:

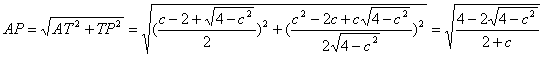
Así,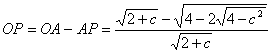

Aquí es donde intento seguir pero.,.. no se qué pasa…

Para que P sea único, debe ser

AE/IP=AO/OP, es decir,

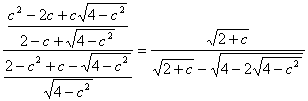
Llevada a Mathematica 6 esta ecuación, nos da tres soluciones:

{{c®-1.92665},{c®1.},{c®0.}}

La solución -1.92665 es absurda en el contexto del problema y la solución 0 crea un triángulo degenerado. La solución c=1, nos da un triángulo 90 60 30.

c=1 resuelve la ecuación:

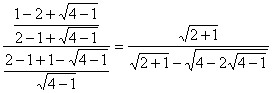, es decir, ,

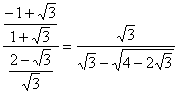O sea: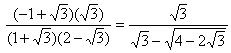

Así es: ,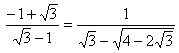

Es decir, hemos de observar que , o sea,

, cqd

Ricardo Barroso Campos

Didáctica de las Matemáticas

Universidad de Sevilla