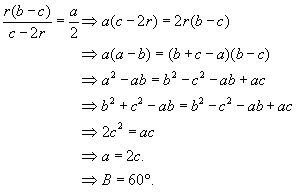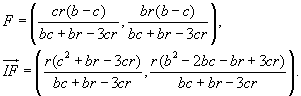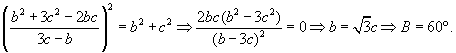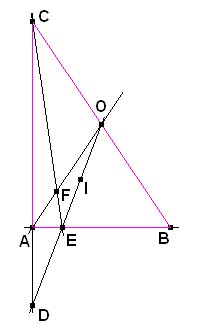
|
Sea ABC un triángulo rectángulo en A, c
< b < a. Trazamos la recta que pasa por el incentro
I, y el circuncentro O, que corta a la prolongación
de AC en D, y AB en E, respectivamente. Probar
si es cierto o no: |
|
Propuesto por Juan Bosco Romero Márquez.
|
Solución de Francisco Javier García Capitán
|
a) Asignemos coordenadas de manera que A=(0,0), B=(c,0), C=(0,b), O=(b/2,c/2) e I=(r,r). A partir de aquí obtenemos: A partir de aquí, que AD = a/2 se expresa |
 |
|
b) Ahora, calculando La segunda coorenadada de este vector debe anularse, por lo que deducimos: Finalmente, imponemos que el triángulo es rectángulo en A: |
|
