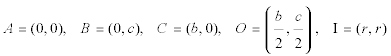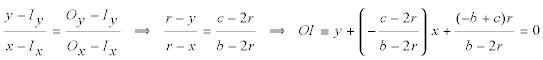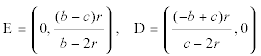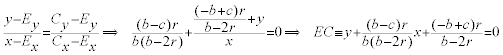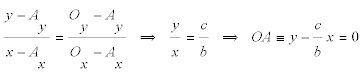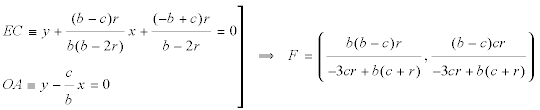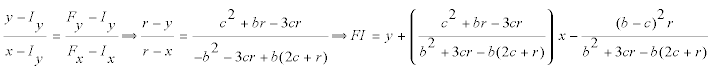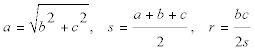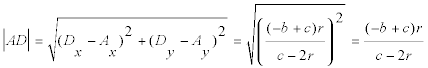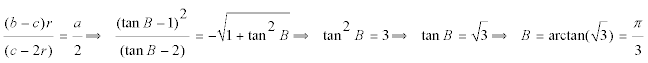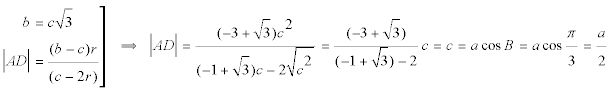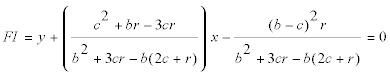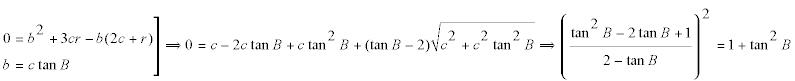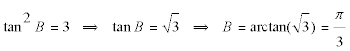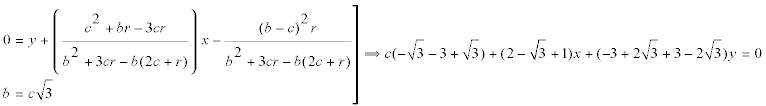|
De investigación. Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid. Problema 421. Sea ABC un triángulo rectángulo en A, c < b < a. Trazamos la recta que pasa por el incentro I, y el circuncentro O, que corta a la prolongación de AC en D y AB en E respectivamente. Probar si es cierto o no:
Romero, J.B. (2007): Comunicación personal. Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (16 noviembre de 2007) |
|
SOLUCIÓN |
|
|
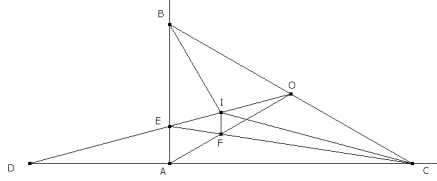
DIBUJAMOS EL ENUNCIADO
Como siempre
Consideramos un sistema coordenado en el que A es el origen, AC el eje de abscisas y AC el eje de ordenadas. En estas condiciones tenemos
donde r es el radio del círculo inscrito. LA RECTA OI
LOS PUNTOS E, D El punto E se obtiene para x=0 en la recta OI y el punto D se obtiene para y=0 en la recta OI
LA RECTA CE
LA RECTA OA
EL PUNTO F El punto F está en la intersección de la recta CE con la recta OA
LA RECTA FI
ÚLTIMOS DETALLES
|
|
SOLUCIÓN DEL APARTADO (a) |
|
|
DIRECTO
Imponemos la condición
RECÍPROCO
|
|
SOLUCIÓN DEL APARTADO (b) |
|
|
ordenamos la ecuación convenientemente
DIRECTO Si IF es paralela a AB es que es paralela al eje de ordenadas y por lo tanto se anula el coeficiente de la y
donde simplificando obtenemos
RECÍPROCO
y simplificando nos queda
que es paralela al eje de ordenadas AB. |