Problema
421
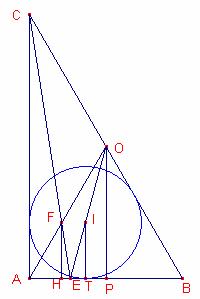
Sea el triángulo
rectángulo 
, 
. Tracemos la recta que pasa por el incentro I y el
circuncentro O, que corta la prolongación del cateto 
en D y el cateto 
en E. Probar si es cierto
o no,
a) 
si y sólo si 
.
b) Sea F la
intersección de 
y 
, entonces 
es paralelo a si y sólo si .
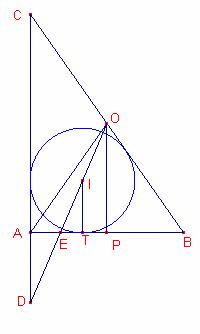
Solución
Ricard Peiró:
El centro
de la circunferencia circunscrita O a un triángulo rectángulo es el punto medio
de la hipotenusa.
Sea P la proyección
de O sobre el cateto .
. 
.
La mediana
referida a la hipotenusa de un triángulo rectángulo es igual a la mitad de la
hipotenusa.
.
Sea T el punto
de tangencia de la circunferencia inscrita y el cateto .
, radio de la circunferencia inscrita.
a)
Supongamos . Sea 
.
Los triángulos
, 
son semejantes. Aplicando
el teorema de Tales:
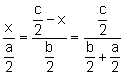, entonces, 
(1)
Los triángulos
, 
son semejantes. Aplicando
el teorema de Tales:
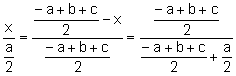, entonces, 
(2)
Igualando
las expresiones (1) (2).
. Simplificando:
. Aplicando el teorema de Pitágoras:
. 
, entonces, .
Supongamos
que .
Entonces, aplicando razones trigonométricas al triángulo rectángulo :
, 
. Sea , 
.
Los triángulos
, son semejantes. Aplicando
el teorema de Tales:
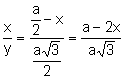(3)
Los triángulos
, son semejantes. Aplicando
el teorema de Tales:
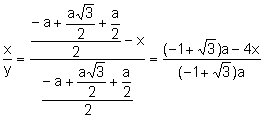(4)
Resolviendo
el sistema formado por las ecuaciones (3) (4)
.
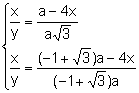
Por tanto
la proposición a) es cierta.
b)
Supongamos
que . 
. , .
Sea H la proyección
de F sobre el cateto .
Por el apartado
a) 
.
Sea 
, 
.
Los triángulos
, son semejantes. Aplicando
el teorema de Tales:
(5)
Los triángulos
, 
son semejantes. Aplicando
el teorema de Tales:
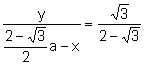(6)
Resolviendo
el sistema formado por las ecuaciones (5) (6)
, 
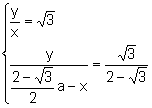Entonces, 
, entonces, es paralelo a .
Sea F la intersección
de y . Sea H la proyección de F sobre el cateto .
Supongamos
que es paralelo a .
Entonces, 
.
Los triángulos
, son semejantes. Aplicando
el teorema de Tales:
.
Los triángulos
, 
son semejantes. Aplicando
el teorema de Tales:
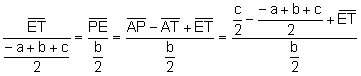
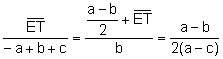. Entonces, 
.
.
Los triángulos
, son semejantes. Aplicando
el teorema de Tales:
.
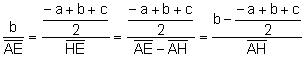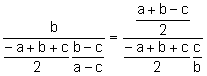, simplificando:
.
.
Aplicando
el teorema de Pitágoras:
.
.
.
.
Entonces, .
Por tanto
la proposición b) es cierta.